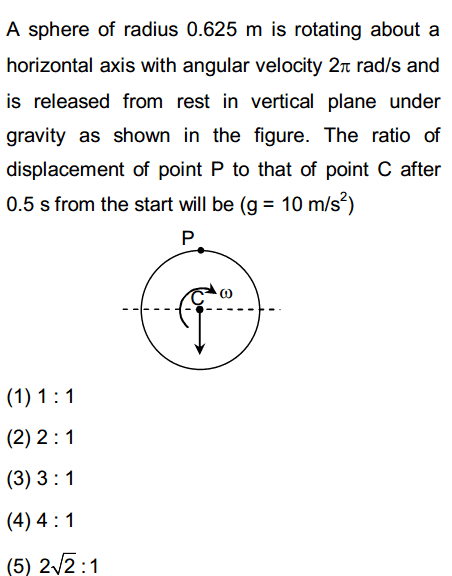
To determine the positions of points P and C after 0.5 seconds, the centripetal acceleration and displacement equations for free-falling bodies are essential. The center of gravity, point C, moves a certain distance downward, while point P's displacement involves calculating the angle using angular velocity. The angular velocity is given in radians per second, allowing for straightforward calculations of the angle traveled by point P. The discussion concludes that the displacement ratio of P to C is 2:1, accounting for the sphere's rotation and downward motion. This analysis effectively combines rotational and translational motion principles.