Finding Global Minima in Likelihood Functions

Click For Summary
SUMMARY

This discussion focuses on finding the global minimum of a likelihood function with multiple local minima. The user seeks basic optimizer principles that can be derived and implemented independently, while also expressing interest in Bayesian optimization methods for obtaining posterior estimates. The conversation highlights the utility of evaluating the function on a fine grid for low-dimensional cases and suggests using local optimizers for increased precision after identifying promising points. The challenges of MCMC sampling due to computational expense are also noted.

PREREQUISITES
  • Understanding of likelihood functions and their properties
  • Familiarity with optimization techniques, particularly global and local optimizers
  • Knowledge of Bayesian optimization principles
  • Basic skills in implementing numerical methods for function evaluation
NEXT STEPS
  • Research basic principles of gradient descent and other local optimization algorithms
  • Explore Bayesian optimization frameworks such as GPyOpt or Scikit-Optimize
  • Learn about grid search techniques for function evaluation in low dimensions
  • Investigate advanced sampling methods to improve MCMC efficiency
USEFUL FOR

Data scientists, statisticians, and machine learning practitioners focused on optimizing likelihood functions and improving model performance through effective optimization strategies.

tworitdash
Messages
104
Reaction score
25
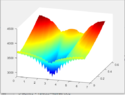
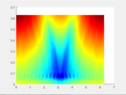
I have a likelihood function that has one global minima, but a lot of local ones too. I attach a figure with the likelihood function in 2D (it has two parameters). I have added a 3D view and a surface view of the likelihood function. I know there are many global optimizers that can be used to obtain the location of the global minimum point in the likelihood function. However, I want to know what basic optimizer principles that I can use (that I can also derive and implement myself) for a problem like this. If you see the 3D view, you may find many local minima. I am also open to suggestions that involve Bayesian type of optimization where I will get a posterior and not just a point estimate. I am open to that as well. I have tried MCMC type sampling optimization, however, they are computationally expensive. The number of parameters may increase later.
 

Attachments

  • cKJT2.png
    cKJT2.png
    19.1 KB · Views: 165
  • 5KeQE.png
    5KeQE.png
    29.2 KB · Views: 157
Physics news on Phys.org
Is it literally just this function you want to optimize?

You already did it, by drawing a graph. More formally if that's unsatisfying, for low dimensions and fast evaluation functions you can just evaluate the function at every point on a fine grid and pick the point with the best value. If you want a little extra precision you can run any optimizer from there to find the local extremum near that point.
 
Reply
  • Like
Likes   Reactions: WWGD and tworitdash

Similar threads

Graduate Constructing PDFs for Max Likelihood Density Estimation Problem
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad What Does the Likelihood Function Tell Us?
  • · Replies 16 ·
Replies
16
Views
2K
Graduate Correlation between parameters in a likelihood fit
  • · Replies 3 ·
Replies
3
Views
2K
MHB Finding MLE for $\theta$ of Statistical Product Model
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad Is the Likelihood Function a Multivariate Gaussian Near a Minimum?
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Maximum Likelihood to find the original data or estimation directly
  • · Replies 8 ·
Replies
8
Views
2K
Undergrad Likelihood of the maximum of a parabola
  • · Replies 2 ·
Replies
2
Views
2K
Solve the Global Minima Problem in Two Variable Functions
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Likelihood of some points fitting a derived function....
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Finding Multiple Local Minima of High-Dimensional Functions
  • · Replies 10 ·
Replies
10
Views
3K