- #1
Terrell
- 317
- 26
I am trying to understand the geometric intuition of the above equation. ##\rho(\tau)## represents the rank of the linear transformation ##\tau## and likewise for ##\rho(\tau\sigma)##. ##Im(\sigma)## means the image of the linear transformation ##\sigma## and lastly, ##K(\tau)## is the kernel of ##\tau##.
The equation: ##\rho(\tau)=\rho(\tau\sigma)+d[Im(\sigma)\cap K(\tau)]##
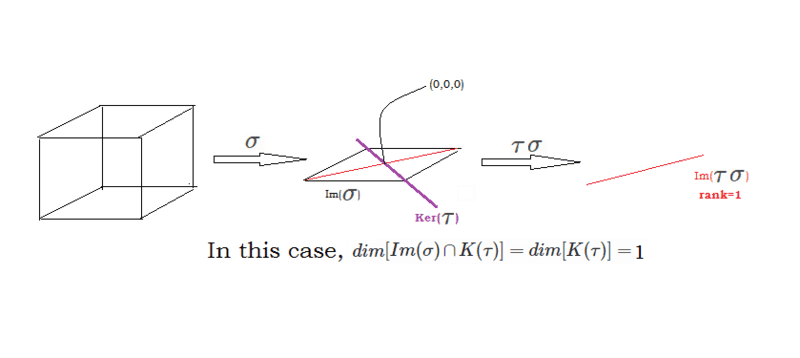
The equation: ##\rho(\tau)=\rho(\tau\sigma)+d[Im(\sigma)\cap K(\tau)]##
Attachments
Last edited: