- #1
Estanho
- 14
- 2
Hi,
I'm developing a data structure to represent 3-D meshes for numeric simulation. I want those meshes to be able to handle any type of polyhedron (not only the classic tetra and hexahedron). The best data structure that I could find was one based on half-edges (or darts), such as this one: https://www.cse.msu.edu/~ytong/papers/halfFace.pdf
The problem is, I want to be able to traverse the faces that compose a given polyhedron, such that this path could be represented as a Hamiltonian cycle on a graph whose nodes are the faces of the polyhedron, and the edges are the face-face connectivity within the polyhedron.
The 2-D counterpart would be a half-edge, which is trivial to traverse as in a Hamiltonian cycle if the graph nodes and edges are the same as the original polygon. All you have to do is follow the half-edges:
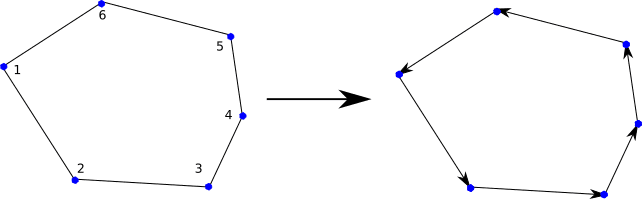
But this doesn't seem to be easy when dealing with faces (or half faces). I don't even know if there will be a hamiltonian path of the faces for every possible polyhedron. And determining those is not easy and hard to keep in memory pre-processed. Here's an example for a prism:
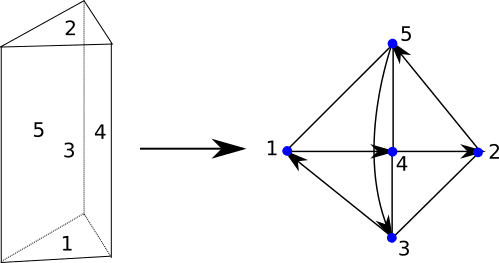
The paper presents a common half-edge, half-face structure to store topological information. This structure allows for some operations (combinatorial maps) on each half-edge: ##\beta_1##, ##\beta_2##, and ##\beta_3##. Those maps are depicted below:
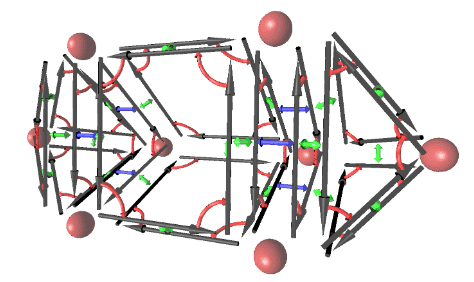
Here, ##\beta_1## is red, ##\beta_2## is green, and ##\beta_3## is blue. So, as you can see, if you apply ##\beta_1## you will get the adjacent half-edge within the same half-face, if you apply ##\beta_2## you will get the adjacent half-edge on an adjacent half-face within the same polyhedron, and if you apply ##\beta_3## you will get the adjacent half-edge on the opposite half-face, from a adjacent polyhedron.
In short, my question is, is there a fast (i.e. with linear complexity) algorithm to traverse all the faces of a given polyhedron using those three operations? It would be sufficient to get just one half-edge for each half-face within the polyhedron, since traversing it is trivial by repeatedly using ##\beta_1##.
Until now, it seems my best bet is a graph-search algorithm, which is way too heavy for my needs.
I'm developing a data structure to represent 3-D meshes for numeric simulation. I want those meshes to be able to handle any type of polyhedron (not only the classic tetra and hexahedron). The best data structure that I could find was one based on half-edges (or darts), such as this one: https://www.cse.msu.edu/~ytong/papers/halfFace.pdf
The problem is, I want to be able to traverse the faces that compose a given polyhedron, such that this path could be represented as a Hamiltonian cycle on a graph whose nodes are the faces of the polyhedron, and the edges are the face-face connectivity within the polyhedron.
The 2-D counterpart would be a half-edge, which is trivial to traverse as in a Hamiltonian cycle if the graph nodes and edges are the same as the original polygon. All you have to do is follow the half-edges:
But this doesn't seem to be easy when dealing with faces (or half faces). I don't even know if there will be a hamiltonian path of the faces for every possible polyhedron. And determining those is not easy and hard to keep in memory pre-processed. Here's an example for a prism:
The paper presents a common half-edge, half-face structure to store topological information. This structure allows for some operations (combinatorial maps) on each half-edge: ##\beta_1##, ##\beta_2##, and ##\beta_3##. Those maps are depicted below:
Here, ##\beta_1## is red, ##\beta_2## is green, and ##\beta_3## is blue. So, as you can see, if you apply ##\beta_1## you will get the adjacent half-edge within the same half-face, if you apply ##\beta_2## you will get the adjacent half-edge on an adjacent half-face within the same polyhedron, and if you apply ##\beta_3## you will get the adjacent half-edge on the opposite half-face, from a adjacent polyhedron.
In short, my question is, is there a fast (i.e. with linear complexity) algorithm to traverse all the faces of a given polyhedron using those three operations? It would be sufficient to get just one half-edge for each half-face within the polyhedron, since traversing it is trivial by repeatedly using ##\beta_1##.
Until now, it seems my best bet is a graph-search algorithm, which is way too heavy for my needs.
