Homology groups with points identified

[dkotschessaa]

I am looking for some general guidance on questions of the form:

"Using a $\Delta$ complex, compute the homology groups of the quotient space obtained fromt the 2-sphere $S^2$ by identifying three of its distinct points."

Similarly I have a question about a torus with two points identified.

I have a pretty good idea of how to compute homology groups with a $\Delta$ complexes now for the Torus, Projective Plane, Klein bottle, etc. But what I am not understanding is what happens when I identify points to one another. i.e. I generally have some polygonal region $I \times I$ divided into triangles, i.e. for the Klein bottle:

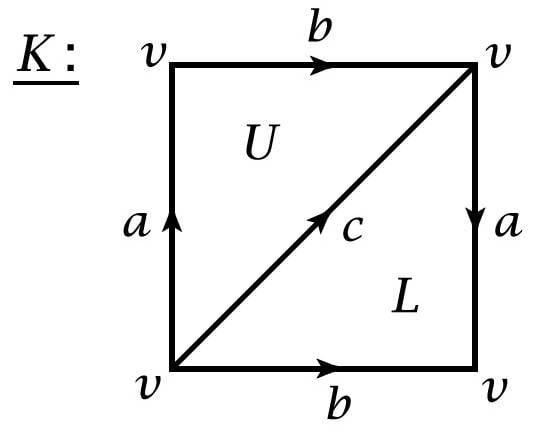
But I don't know what happens to t his structure when I pick some points on them and start identifying them. What does my complex look like?

-Dave K

 

[lavinia]

If you want to use simplicial homology you would have to retriangulate the space.

BTW: Your diagram is not a triangulation of the Klein bottle.

If you use Singular Homology then the Meyer-Vietoris sequence is the ticket.

 

[dkotschessaa]

If you want to use simplicial homology you would have to retriangulate the space.

BTW: Your diagram is not a triangulation of the Klein bottle.

If you use Singular Homology then the Meyer-Vietoris sequence is the ticket.

The picture indicated is a $\Delta$ complex - it's the one from Hatcher. So, definitely a Klein bottle, not necessarily a triangulation.

I am also still sorting out CW-complexes, vs. $\Delta$ complexes , singular vs. simplicial homology and such ,so bear with me.

But the question does ask specifically about the $\Delta$ complexes.

-Dave K

 

[lavinia]

The picture indicated is a $\Delta$ complex - it's the one from Hatcher. So, definitely a Klein bottle, not necessarily a triangulation.

I am also still sorting out CW-complexes, vs. $\Delta$ complexes , singular vs. simplicial homology and such ,so bear with me.

But the question does ask specifically about the $\Delta$ complexes.

-Dave K

What is a Δ complex?

 

[dkotschessaa]

What is a Δ complex?

I don't know of a very concise definition, sorry. It's on page 102 in Hatcher.

 

[lavinia]

I don't know of a very concise definition, sorry. It's on page 102 in Hatcher.

If I understand it right, a simplicial complex is a Δ-complex. So you could triangulate the space.

You can also notice that attaching a 1 cell with its endpoints to two different vertexes of the surface is homotopically equivalent to identifying the two points.

Take a point in the interior of an n-simplex and subdivide the n simplex with that point as a new vertex. Do the same for the second point in the interior of another simplex. Then identify the two points.

 

[dkotschessaa]

If I understand it right, a simplicial complex is a Δ-complex. So you could triangulate the space.

You can also notice that attaching a 1 cell with its endpoints to two different vertexes of the surface is homotopically equivalent to identifying the two points.

Take a point in the interior of an n-simplex and subdivide the n simplex with that point as a new vertex. Do the same for the second point in the interior of another simplex. Then identify the two vertices.

Thanks for your reply. I was starting to suspect that about the 1 cell. I'll give it a try and get back to you!

 

[lavinia]

Thanks for your reply. I was starting to suspect that about the 1 cell. I'll give it a try and get back to you!

The third paragraph was another way of doing it without attaching a 1 cell.

 

[WWGD]

If you want to use simplicial homology you would have to retriangulate the space.

BTW: Your diagram is not a triangulation of the Klein bottle.

If you use Singular Homology then the Meyer-Vietoris sequence is the ticket.

Doesn't MV apply to all "non-extraordinary" theories?

 

[lavinia]

Doesn't MV apply to all "non-extraordinary" theories?

I would think that you would still need to subdivide to get neighborhoods of the identified points. But I am not sure how to do Meyer-Vietoris in simplicial homology - this because simplices are not open sets. Can you explain?

 

[WWGD]

I would think that you would still need to subdivide to get neighborhoods of the identified points. But I am not sure how to do Meyer-Vietoris in simplicial homology - this because simplices are not open sets. Can you explain?

Good point, let me think it through some more.

 

[mathwonk]

Using Lavinia's nice remarks, I think one can see that a sphere with three points identified is homotopically the same as a "sphere with (two) earrings", an example Bott gave us to illustrate that homology does not disinguish between spaces all that well. I.e. this has the same homology as a 2-torus.

In general the easiest way for me to compute homology is by the inductive formulas for how it changes under attaching cells. This allowed me e.g. to compute fairly easily the homology of the real grassmannian G(2,4) of real 2-planes (through the origin) in real 4-space, or equivalently the space of projective lines in projective 3-space. These formulas are no doubt a corollary of mayer vietoris sequences, the standard tool.

I like explicit hands - on methods like triangles for getting a concrete feel, but I always recall the remark by Dold that using them to compute homology is like using riemann sums to compute integrals. Of course i do that too, at least at first.

 

[WWGD]

If you had just identified two points , I think your pace would be homotopic to an $S^1$ attached to an $S^2$ , but with three points it seems you could attach a half of an $S^1$ to the first handle or some variant of it?

 

[WWGD]

I would think that you would still need to subdivide to get neighborhoods of the identified points. But I am not sure how to do Meyer-Vietoris in simplicial homology - this because simplices are not open sets. Can you explain?

Maybe using simplicial maps which themselves can be approximated by continuous functions?

 

[lavinia]

Maybe using simplicial maps which themselves can be approximated by continuous functions?

Not sure what you mean. I will look up how the excision axiom is satisfied in simplicial homology.

 

[WWGD]

Not sure what you mean. I will look up how the excision axiom is satisfied in simplicial homology.

Do you mean a specific argument that we can remove subspaces and then the inclusion induces an isomorphism ? Or a specific example:
How about this, consider a ball , i.e., a 2-simplex :=X , a given point * in the interior of X and a disk D within X containing * , i.e., Y:=X-D , then

$\mathbb Z =H_2( X, X- {pt}) =H_2( X-Y, (X-{pt}) -Y)=H_2(D, D-{pt})$?

 

[lavinia]

Do you mean a specific argument that we can remove subspaces and then the inclusion induces an isomorphism ? Or a specific example:
How about this, consider a ball , i.e., a 2-simplex :=X , a given point * in the interior of X and a disk D within X containing * , i.e., Y:=X-D , then

$\mathbb Z =H_2( X, X- {pt}) =H_2( X-Y, (X-{pt}) -Y)=H_2(D, D-{pt})$?

right but if you remove one a point it is no longer a simplicial complex

 

[WWGD]

right but if you rem one a point it is no longer a simplicial complex

But, can we work up to homotopy? D-{pt} retracts to the boundary S^1 , which is a simplex without its interior? EDIT: Or must each step of the homotopy(retract) be represented by a simplex?

 

[lavinia]

not sure

 

[dkotschessaa]

This shouldn't need an MV sequence to do since 1) we never learned it and 2) the question is about $\Delta$ complexes. It should be fairly straightforward. I'm still just not sure what the complex should look like. i.e. I don't know what represents two points being identified on it.

 

[lavinia]

This shouldn't need an MV sequence to do since 1) we never learned it and 2) the question is about $\Delta$ complexes. It should be fairly straightforward. I'm still just not sure what the complex should look like. i.e. I don't know what represents two points being identified on it.

I explained in the first post that you need to subdivide the complex so that the two identified points are vertexes and then identify them.

BTW: Did you learn Excision?
The Meyer Vietoris sequence is incredibly important. I suggest that you learn it.

 

[dkotschessaa]

I explained in the first post that you need to subdivide the complex so that the two identified points are vertexes and then identify them.

Oh, you did say to retriangulate, but that was all you said . So I didn't understand about the vertices. That makes more sense though and I will give it a try.

BTW: Did you learn Excision?

No.

The Meyer Vietoris sequence is incredibly important. I suggest that you learn it.

I believe you, but I don't have the luxury of time to go outside the tested material. In fact I have... 37 days!