How does the Triangle Inequality apply in this situation?

[Seydlitz]

I'm beginning to read Spivak's Calculus 3ed, and everything is smooth until I reach page 12.

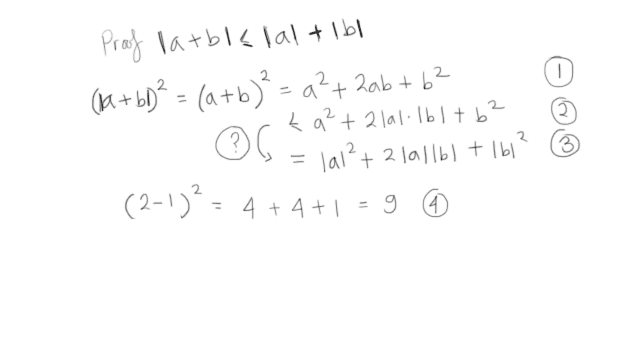
My question is marked, between line 2 and 3. Why there's such sign change suddenly? In fact I tried with simple line 4 case and it's not in fact equal. I'm assuming that a and b is valid for all integer case whether they are negative or not.

Then I read this:
http://math.ucsd.edu/~wgarner/math4c/derivations/other/triangleinequal.htm
(Please see to the Alternative Proof of the Triangle Inequality section)

It clearly contradicts what Spivak's book said in line 3. Then I think, whether he intends to do the case where a and b are both positive, but then the question arises why there's larger than sign in line 2 if that's the case.

Thanks

 

[jbunniii]

To go from line 1 to line 2, note that for any real number $x$, we have $x \leq |x|$. In particular, for $x = ab$, we have $ab \leq |ab|$. But of course $|ab| = |a| \cdot |b|$, so the inequality becomes $ab \leq |a| \cdot |b|$. We may now multiply this by 2, and add $a^2 + b^2$ to both sides to obtain
$$a^2 + 2ab + b^2 \leq a^2 + 2|a| \cdot |b| + b^2$$
To go from line 2 to 3, we simply recognize that since $a$ and $b$ are real, we have $a^2 = |a|^2$ and $b^2 = |b|^2$. Therefore the right hand side of the above inequality is equal to $|a|^2 + 2 |a| \cdot |b| + |b|^2$.

Combining all of the above, we conclude that
$$\begin{align}a^2 + 2ab + b^2 &\leq a^2 + 2|a| \cdot |b| + b^2 \\
&= |a|^2 + 2|a| \cdot |b| + |b|^2\end{align}$$
The proof at your link carries out the same steps, but in a different order, which is why the $\leq$ appears later.

Note that the $=$ sign in the above chain does NOT mean that all of the expressions are equal. Only the expressions immediately before and after the $=$ sign are equal. Since there is at least one $\leq$ in the chain, the correct conclusion is
$$(|a|+|b|)^2 \leq |a|^2 + 2|a| \cdot |b| + |b|^2$$
not
$$(|a|+|b|)^2 = |a|^2 + 2|a| \cdot |b| + |b|^2$$

 

[Seydlitz]

To go from line 1 to line 2, note that for any real number $x$, we have $x \leq |x|$. In particular, for $x = ab$, we have $ab \leq |ab|$. But of course $|ab| = |a| \cdot |b|$, so the inequality becomes $ab \leq |a| \cdot |b|$. We may now add $a^2 + b^2$ to both sides to obtain
$$a^2 + ab + b^2 \leq a^2 + |a| \cdot |b| + b^2$$
To go from line 2 to 3, we simply recognize that since $a$ and $b$ are real, we have $a^2 = |a|^2$ and $b^2 = |b|^2$. Therefore the right hand side of the above inequality is equal to $|a|^2 + |a| \cdot |b| + |b|^2$.

Combining all of the above, we conclude that
$$\begin{align}a^2 + ab + b^2 &\leq a^2 + |a| \cdot |b| + b^2 \\
&= |a|^2 + |a| \cdot |b| + |b|^2\end{align}$$
The proof at your link carries out the same steps, but in a different order, which is why the $\leq$ appears later.

Ah ok! I get what you're explaining. It seems clearer now. What I didn't get is the fact that the sign in line 2 is 'nested' to that of line 3. Not to the first original expression on the far left. You left out the factor 2 also but I assumed we can just multiply that in and adds $a^2$ and $b^2$, in the beginning of your explanation.

(I was quite sleepy perhaps, sorry)

Note that the $=$ sign in the above chain does NOT mean that all of the expressions are equal. Only the expressions immediately before and after the $=$ sign are equal. Since there is at least one $\leq$ in the chain, the correct conclusion is
$$(|a|+|b|)^2 \leq |a|^2 + |a| \cdot |b| + |b|^2$$
not
$$(|a|+|b|)^2 = |a|^2 + |a| \cdot |b| + |b|^2$$

Do you mean the last part as this?
$$(|a+b|)^2 \neq |a|^2 + 2|a| \cdot |b| + |b|^2$$

Because I think this is true. (I added the missing 2, because without it even the first inequality wouldn't hold)
$$(|a|+|b|)^2 = |a|^2 + 2|a| \cdot |b| + |b|^2$$

and thus
$$(|a+b|)^2 \leq |a|^2 + 2|a| \cdot |b| + |b|^2 = (|a|+|b|)^2$$

Thanks for your help!

 

[jbunniii]

Yes, sorry, I left the 2 out of both expressions. I'll edit my post now to avoid confusion.

 

[jbunniii]

Ah ok! I get what you're explaining. It seems clearer now. What I didn't get is the fact that the sign in line 2 is 'nested' to that of line 3. Not to the first original expression on the far left.

Yes, that's right. In general, something of the form $X \leq Y = Z$ means "$X \leq Y$ and $Y = Z$", from which it follows that $X \leq Z$.