How Is Trigonometry Used to Calculate Flagpole Heights?

[ai93]

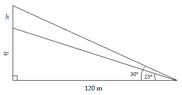
A vertical flagpole is fixed at the top of a vertical wall. From a point which is 120m measured horizontally from the base of the wall the angle of elevation to the top of the flagpole is 30 degrees, and the angle of elevation to the bottom of the flagpole is 25 degrees.

a) Draw a clearly labelled diagram to represent this situation

b) Calculate the length of the flagpole correct to 2 dp

View attachment 3811

I have attempted to draw the diagram, and hopefully figured the height out. Although I could be completely wrong!

 

[MarkFL]

I would draw the diagram as follows:

View attachment 3812

From this, we see:

\(\displaystyle \tan\left(25^{\circ}\right)=\frac{w}{120}\tag{1}\)

\(\displaystyle \tan\left(30^{\circ}\right)=\frac{w+h}{120}\tag{2}\)

Now, can you use (1) to eliminate $w$ in (2)?

 

[ai93]

I would draw the diagram as follows:

View attachment 3812

From this, we see:

\(\displaystyle \tan\left(25^{\circ}\right)=\frac{w}{120}\tag{1}\)

\(\displaystyle \tan\left(30^{\circ}\right)=\frac{w+h}{120}\tag{2}\)

Now, can you use (1) to eliminate $w$ in (2)?

\(\displaystyle \tan\left(25^{\circ}\right)=\frac{w}{120}\tag{1}\)

\(\displaystyle w=tan(25)x120=55.95\)

\(\displaystyle tan(30)=\frac{55.95+h}{120}\)

\(\displaystyle \therefore tan(30) \cdot 120 = 55.95+h\)

\(\displaystyle 69.28+55.95+h\)

\(\displaystyle 69.28-55.95=h\)

\(\displaystyle \therefore h=13.33\)

I think that's right

- - - Updated - - -

If I am given a similar question with two angles. The biggest angle would obviously be the outer angle?

 

[MarkFL]

I would rewrite (2) as:

\(\displaystyle \tan\left(30^{\circ}\right)=\frac{w}{120}+\frac{h}{120}\)

Then use (1) to obtain:

\(\displaystyle \tan\left(30^{\circ}\right)=\tan\left(25^{\circ}\right)+\frac{h}{120}\)

And then solving for $h$, we get (in meters):

\(\displaystyle h=120\left(\tan\left(30^{\circ}\right)-\tan\left(25^{\circ}\right)\right)\approx13.33\)

Your answer is correct, however, it is best to obtain the exact value first, and then only at the very end do your rounding. Sometimes intermediary rounding can cause your end result to be inaccurate.

Regarding which angle is larger, we know that if two rays have the same terminus, but one passes through a higher point over the same horizontal distance, then its angle of elevation must be greater. :D

 

[CellCoree]

a) The diagram would look like this:

30°
/|
/ |
/ |h
/ |
/ |
/ |
/ |
/ |
/ |
/_________|
120m

b) To calculate the length of the flagpole, we can use the trigonometric ratio tangent. We know that the tangent of an angle is equal to the opposite side divided by the adjacent side. In this case, the tangent of 30 degrees is equal to the height of the flagpole (opposite side) divided by 120m (adjacent side). So we can set up the equation:

tan(30°) = h/120m

To solve for h, we can multiply both sides by 120m:

120m * tan(30°) = h

Using a calculator, we get:

120m * 0.5774 = h

So the height of the flagpole is approximately 69.29m. Therefore, the length of the flagpole is 69.29m + 120m = 189.29m, rounded to 2 decimal places.