member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For 6(b),
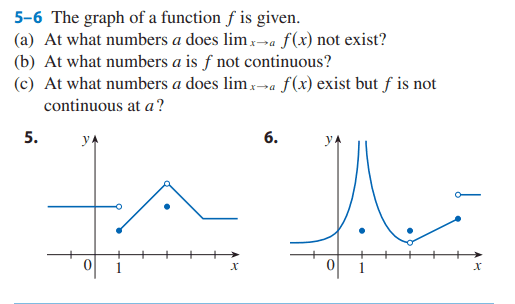
The solution is,

However, for ##a = 1## they could have also said that f is not continuous since f(1) is not defined (vertical asymptote) correct?
Many thanks!
The solution is,
However, for ##a = 1## they could have also said that f is not continuous since f(1) is not defined (vertical asymptote) correct?
Many thanks!