- #1
Andrei1
- 36
- 0
I would like to discuss the following problem.
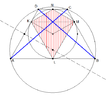
The quadrilateral \(\displaystyle ABCD\) is inscribed into a circle of given radius \(\displaystyle R.\) And it is circumscribed to a circle. The tangent points from the second circle produce another quadrilateral \(\displaystyle KLMN\) such that \(\displaystyle S_{ABCD}=3S_{KLMN}.\) Also \(\displaystyle \gamma\) is the angle between diagonals \(\displaystyle AC\) and \(\displaystyle BD.\) Find the area of \(\displaystyle ABCD.\)
I have no ideas. I wonder if I have to search any regularities of \(\displaystyle ABCD.\) All given elements seem to me "distanced" from each other.
The quadrilateral \(\displaystyle ABCD\) is inscribed into a circle of given radius \(\displaystyle R.\) And it is circumscribed to a circle. The tangent points from the second circle produce another quadrilateral \(\displaystyle KLMN\) such that \(\displaystyle S_{ABCD}=3S_{KLMN}.\) Also \(\displaystyle \gamma\) is the angle between diagonals \(\displaystyle AC\) and \(\displaystyle BD.\) Find the area of \(\displaystyle ABCD.\)
I have no ideas. I wonder if I have to search any regularities of \(\displaystyle ABCD.\) All given elements seem to me "distanced" from each other.