Internal energy won't add up to 0 in cyclic process

[giraffe714]

Homework Statement

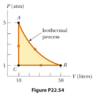
A 1.00-mol sample of an ideal monatomic gas is taken through the cycle shown in Figure P22.54. The process A -> B is a reversible isothermal expansion.
(e) Calculate the changes in internal energy for each process.

Relevant Equations

ΔU_isothermal = 0, ΔU_isobaric = nC_P*ΔT, ΔU_isochoric = nC_V*ΔT, ΔU = Q + W (maybe?), PV = nRT

My problem isn't exactly with calculating the actual changes in internal energy, I'll put those values below. My problem is that I can't get the values to add up to 0, and I don't understand why since for cyclic processes, by definition, ΔU must equal 0.

$$ΔU_{AB} = ΔU_{isothermal} = 0$$
$$ΔU_{BC} = ΔU_{isobaric} = nC_PΔT_{BC} = n\frac{R}{1 - 1/γ}(T_C - T_B) = 1\frac{8.314}{1 - 1/(5/3)}(122 - 609) = -10122 \text{ J}$$
$$ΔU_{CA} = ΔU_{isochoric} = nC_VΔT_{CA} = n\frac{R}{γ - 1}(T_A - T_C) = 1\frac{8.314}{5/3 - 1}(609 - 122) = 6073\text{ J}$$

Which doesn't add up to 0 like it should for a cyclic process. What am I missing here? I feel like something with the "reversible" isothermal process but I'm not sure? And in case you're wondering where I got the values 122 and 609 from for the temperatures, I calculated them using PV = nRT:

$T_A = \frac{P_A*V_A}{nR} = \frac{5*101325*10*0.001}{1*8.314} = 609\text{ K}$ (here I'm converting atm to Pa and L to m^3)
Now since A -> B is isothermal $T_B = T_A = 609\text{ K}$
$T_C = \frac{1*101325*10*0.001}{1*8.314} = 122\text{ K}$

 

[giraffe714]

Okay, so I figured it out, I was using the wrong equation for ΔU_isobaric, it's still $nC_VΔT$, I got that formula confused with the one for heat transfer in an isobaric process, $Q = nC_PΔT$.