- #1
Happiness
- 679
- 30
If ##t## is a function of ##r##, then we may in theory find ##r## as a function of ##t##, as claimed in the last paragraph of the attachment below. My issue is this is only true if ##t## is a 1-1 function of ##r##. Otherwise, suppose ##t=r^2##. Then ##r=\pm\sqrt{t}##, which isn't a function.
I understand that physically it makes no sense for ##t## not to be a 1-1 function of ##r##, because we would then have two different values of ##r## at a particular time and an object can't be at two places at once. But mathematically, I don't see how (6.15) shows ##t## is a 1-1 function of ##r##.
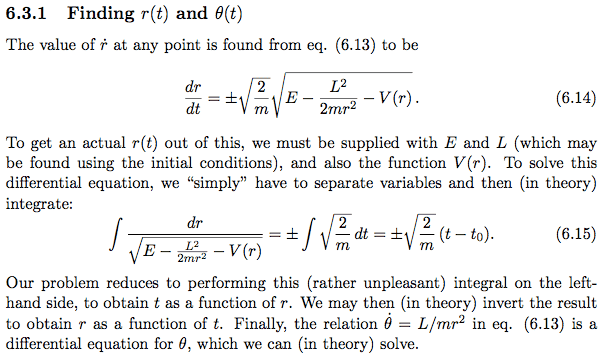
I understand that physically it makes no sense for ##t## not to be a 1-1 function of ##r##, because we would then have two different values of ##r## at a particular time and an object can't be at two places at once. But mathematically, I don't see how (6.15) shows ##t## is a 1-1 function of ##r##.