Ngineer
- 62
- 1
Hi everyone,
Someone posted this hypothetical problem on a facebook group and I am wondering what your thoughts are.
The issue is that Snell's law does not seem to hold when applied to the transmitted wave (calculated using the electromagnetic interface conditions.) Here is an example:
Suppose we have an interface at y=0 between vacuum (medium 1; n1 = 1) and a material of εr = μr = 10 (medium 2; n2 = 10).
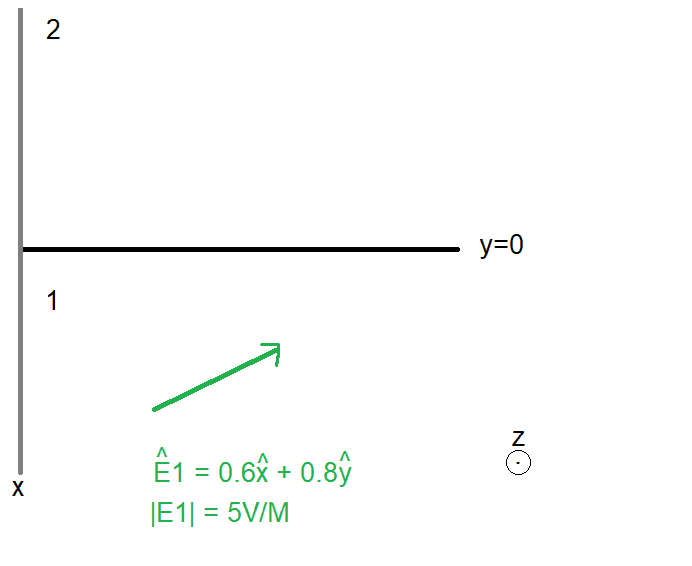
For a plane electromagnetic wave whose electric field is given by the green arrow, we subsequently have:

And a propagation direction along E1xH1:
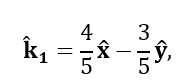
which corresponds to an angle of 36.87 degrees.
Using the interface conditions, we find that in the second medium, E2 has a unit vector of (x+ 0.132y), and that H2 is in a direction identical to H1 (i.e. z).
This gives rise to a propagation direction of
k2 = -0.132x + y
Which corresponds to an angle of 82.47 degrees.
Now the problematic issue is:
sin(theta2) / sin(theta1) = sin(82.47)/sin(36.87) = 1.65
Whereas
n1/n2 = 1/10 = 0.1.
Doesn't Snell's law stipulate that they're equal? What went wrong?
Someone posted this hypothetical problem on a facebook group and I am wondering what your thoughts are.
The issue is that Snell's law does not seem to hold when applied to the transmitted wave (calculated using the electromagnetic interface conditions.) Here is an example:
Suppose we have an interface at y=0 between vacuum (medium 1; n1 = 1) and a material of εr = μr = 10 (medium 2; n2 = 10).
For a plane electromagnetic wave whose electric field is given by the green arrow, we subsequently have:
And a propagation direction along E1xH1:
which corresponds to an angle of 36.87 degrees.
Using the interface conditions, we find that in the second medium, E2 has a unit vector of (x+ 0.132y), and that H2 is in a direction identical to H1 (i.e. z).
This gives rise to a propagation direction of
k2 = -0.132x + y
Which corresponds to an angle of 82.47 degrees.
Now the problematic issue is:
sin(theta2) / sin(theta1) = sin(82.47)/sin(36.87) = 1.65
Whereas
n1/n2 = 1/10 = 0.1.
Doesn't Snell's law stipulate that they're equal? What went wrong?
