- #1
bobby2k
- 127
- 2
Is there a "Leibnitz theorem" for sums with variable limits?
Wikipedia says that if we want to differentiate integrals where the variable is in the limit and in the integrand, we can use Leibnitz theorem:
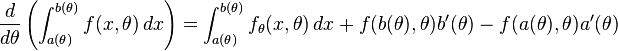
But what if I need to integrate a function defined like this:[itex]\Sigma_{I(x)}[f(x,t)][/itex], Here I(x) just means that the values depend on x. Or even what if I simpler:
[itex]\Sigma^{b(x)}_{a(x)}[f(x,t)][/itex], where we just have that the start and end of the summation depend on x. Are there some conditions where if we want to calculate:
[itex]\frac{d}{dx}[\Sigma_{I(x)}[f(x,t)]][/itex], we can move move the derivative inside, and get some more terms. Or do we have to calculate the sum before differentiating?
Wikipedia says that if we want to differentiate integrals where the variable is in the limit and in the integrand, we can use Leibnitz theorem:
But what if I need to integrate a function defined like this:[itex]\Sigma_{I(x)}[f(x,t)][/itex], Here I(x) just means that the values depend on x. Or even what if I simpler:
[itex]\Sigma^{b(x)}_{a(x)}[f(x,t)][/itex], where we just have that the start and end of the summation depend on x. Are there some conditions where if we want to calculate:
[itex]\frac{d}{dx}[\Sigma_{I(x)}[f(x,t)]][/itex], we can move move the derivative inside, and get some more terms. Or do we have to calculate the sum before differentiating?