Aristotle
- 169
- 1
Hi, I was just looking at an example for a certain problem and noticed that in the second step they went to arctan(epsilon). I know there's a form that is equal to arctan but am a little unsure.
I've come across formulas on the web such as
arctan(x) = ∫(dt)/(a2+t2)
but nothing else that would get to arctan.
Can somebody please direct me to the correct formula?
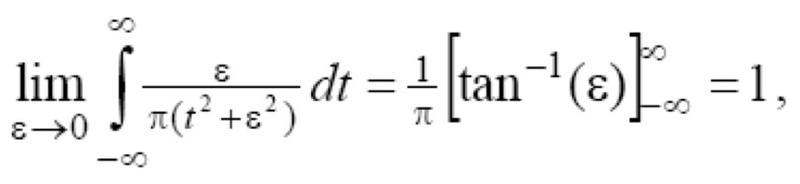
I've come across formulas on the web such as
arctan(x) = ∫(dt)/(a2+t2)
but nothing else that would get to arctan.
Can somebody please direct me to the correct formula?
