Need help with a proof involving points on a quadratic

[Jeff.Nevington]

TL;DR Summary

Given three points on a positive definite quadratic line, I need to prove that the middle point is never higher than at least one of the other two.

Summary: Given three points on a positive definite quadratic line, I need to prove that the middle point is never higher than at least one of the other two.

I am struggling to write a proof down for something. It's obvious when looking at it graphically, but I don't know how to write the proof succinctly.

I have a positive definite quadratic equation:

y= (αx + φ)^2+x^2;
where x and y are the axes, and α and φ are real constants (could be positive or negative), so y is always ≥0.

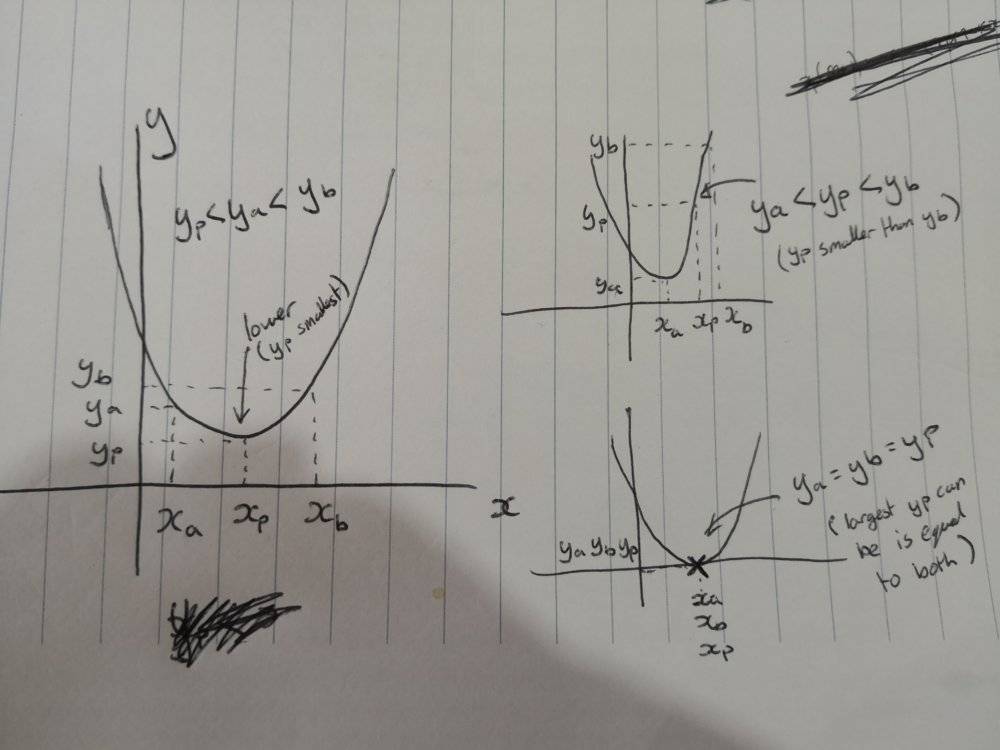
If I choose three values of X: x_a, x_p, x_b, these will correspond to three values of y: y_a, y_p, y_b.
If x_a ≤ x_p ≤ x_b, it is obvious, visually on the curve that y_p ≤ y_a OR y_p ≤ y_b. Unfortunately I need something more robust than "obvious visually". Does anyone know how I would go about writing a mathematical proof for this?

 

[mfb]

Your parabola has an absolute minimum (you can find it but you don't need to), its derivative is negative for smaller x-values and positive for larger values. If the middle point is to the left of the absolute minimum, which point is guaranteed to be larger (in y) than the middle point? If the middle point is to the right of the absolute minimum, which point is guaranteed to be larger than the middle point? What if the middle point is at the absolute minimum?

 

[Jeff.Nevington]

Your parabola has an absolute minimum (you can find it but you don't need to), its derivative is negative for smaller x-values and positive for larger values. If the middle point is to the left of the absolute minimum, which point is guaranteed to be larger (in y) than the middle point? If the middle point is to the right of the absolute minimum, which point is guaranteed to be larger than the middle point? What if the middle point is at the absolute minimum?

Thank you, so I can write:

let x_m be the x value at the absolute minimum;
for x_p ≥ x_m and for x ≥ x_p; dy/dx ≥ 0, hence y_b ≥ y_p as x_b ≥ x_p;
for x_p ≤ x_m and for x ≤ x_p; dy/dx ≤ 0, hence y_a ≥ y_p as x_a ≤ x_p;

I think these two cover everything and I don't necessarily need a 3rd statement considering only x_p=x_m?

Does the above qualify as a proof?

 

[mfb]

Right.

 

[PeroK]

Thank you, so I can write:

let x_m be the x value at the absolute minimum;
for x_p ≥ x_m and for x ≥ x_p; dy/dx ≥ 0, hence y_b ≥ y_p as x_b ≥ x_p;
for x_p ≤ x_m and for x ≤ x_p; dy/dx ≤ 0, hence y_a ≥ y_p as x_a ≤ x_p;

I think these two cover everything and I don't necessarily need a 3rd statement considering only x_p=x_m?

Does the above qualify as a proof?

It must be true for any quadratic with positive coefficient of $x^2$. We can write:

$y = ax^2 + bx + c = a[(x - b/2a)^2 + k]$

For some constant $k$.

We can see that $y(x_1) > y(x_2)$ iff $(x_1 - b/2a)^2 > (x_2 - b/2a)^2$.

Now consider the cases where the middle point is greater or less than $b/2a$.

That, it seems to me, gets at the heart of the matter.