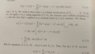Proof of dimension of the tangent space

[hideelo]

I am attaching a picture of a proof from the book "general relativity" by wald. This is supposed to show that the tangent space of an n dimensional manifold is also n dimensional. I have two questions.

In equation 2.2.3 couldn't the function be anything at a since the (x-a) term is 0?

How is the equality in equation 2.2.5 justified, I'm just not seeing it

 

[micromass]

I'm sorry, I cannot read the picture attached. Can't you just type it?

 

[hideelo]

It's hard to write them out on my phone, so I'll try another picture

 

[hideelo]

Is that better?

 

[martinbn]

No, it has to be exacly as written. Otherwise 2.2.2. will not be true.

 

[hideelo]

I'm assuming 2.2.2 follows from the gradient theorem, in which case 2.2.3 should really be an integral, otherwise it's not an equality but the linear approximation.

 

[Fredrik]

A proof very similar to Wald's is included in Isham. Start reading on page 79. The proof is on pages 82-84.

Last time I discussed this proof with someone, I posted my version of it. It's in post #14 here.

 

[Fredrik]

In equation 2.2.3 couldn't the function be anything at a since the (x-a) term is 0?

The theorem says that the function is smooth, i.e. differentiable an arbitrary number of times. Differentiable functions are continuous. The value of a continuous function at a specific point in its domain is completely determined by its values in the rest of its domain. For example, if $f:\mathbb R\to\mathbb R$ is continuous then $f(0)=\lim_{n\to\infty}f\big(\frac 1 n\big)$.

How is the equality in equation 2.2.5 justified, I'm just not seeing it

Assuming that you meant the last equality, this is how:

First term: f(p) is a constant function (the map that takes an arbitrary q to f(p)), so v(f(p))=0.

Second term: The sum is of the form $\sum_\mu (A_\mu-A_\mu)B_\mu$ so every term is zero.

Third term: For all smooth functions f and all constant functions g, we have v(f-g)=v(f)-v(g)=v(f).

 

[mathwonk]

an n manifold is by definition locally isomorphic (i.e. diffeomorphic)) to R^n, hence (by chain rule) each tangent space is isomorphic to the tangent space to R^n at the image point. Do you know that R^n is the tangent space to R^n at each point? That would do it.