- #1
The_Logos
- 8
- 0
Does anybody knows how you can reach one form of the divergence formula from the other? Or in general, why is the equivalence
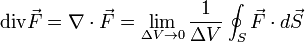 true?
true?
The formula is a direct consequence of Gauss' divergence theorem. You may look at the things in the following manner.The_Logos said:Does anybody knows how you can reach one form of the divergence formula from the other? Or in general, why is the equivalencetrue?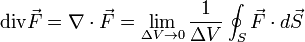
mathman said:
zoki85 said:The formula is a direct consequence of Gauss' divergence theorem. You may look at the things in the following manner.
Suppose p is a point in 3D Euclidean space. Let Er be a solid ball centered at p with radius r , and let Sr be the boundary surface of Er with outward pointing normal (and F is the vector field). Using Gauss' theorem we have:
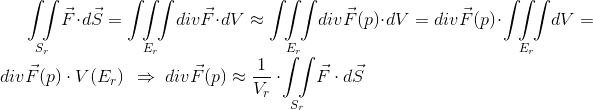
This aproximation improves as radius gets smaller, and in the limit (for r → 0 ⇒ Vr → 0) the equality holds.
Hope this helps.
Meh, my "logos" is quite irrational in everyday life, so I don't think that user name would suit me fine. And, althought short, this is kind of a sloppy proof. It's more a demonstration by Gauss' D.T. why it holds true. I guess a pro-mathematcian should feel a need to "polish" it, to write more rigouros proof. I agree there must be other ways to prove the formula (without G.D.T.) but I didn't try it.The_Logos said:That is just beautiful! you should just go ahead and take my user name, you are definitely more the logos than me! I wasted all day trying to make linear transformations thinking that it was my only hope (And managed nothing).
I actually was seeking for the proof of the equivalence before giving deep thought to the divergence theorem, just to find out that ironically I needed it to prove what apparently came before!.
The nabla form of Divergence is a mathematical representation of the flux of a vector field through a small surface surrounding a given point. It is denoted by the symbol ∇⋅ and is also known as the "del dot" operator.
The integral form of Divergence is a way to calculate the flux of a vector field through a closed surface by integrating the divergence of the field over the surface. It is represented by the integral symbol ∫ and is also known as Gauss's Theorem or the Divergence Theorem.
The two forms of Divergence are equivalent, meaning they convey the same information and can be transformed into each other using mathematical operations. This equivalence is known as the Proof of Equivalence between nabla form and integral form of Divergence.
The Proof of Equivalence between nabla form and integral form of Divergence is important because it allows us to use either form to solve problems in physics and engineering. It also demonstrates the fundamental relationship between the concepts of flux and divergence in vector calculus.
The Proof of Equivalence between nabla form and integral form of Divergence is derived using mathematical techniques, such as the Divergence Theorem and vector identities, to transform one form into the other. The proof is based on the fundamental theorem of calculus and the definition of divergence.