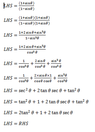Prove Identity: (1+sin(x))/(1-sin(x))=2tan^2(x)+1+2tan(x)sec(x)

[Sean1]

I cannot seem to prove the following identity

(1+sin(x))/(1-sin(x))=2tan^2(x)+1+2tan(x)sec(x)

Can you assist?

 

[Jameson]

Hi Sean,

Let's start with the left-hand side.

$$\frac{1+\sin(x)}{1-\sin(x)}$$.

We want this to turn into an expression without a fraction, so maybe we can try getting rid of the denominator somehow. When I see something in the form of $a-b$, I often try multiplying by the conjugate $a+b$.

$$\frac{1+\sin(x)}{1-\sin(x)} \left( \frac{1+\sin(x)}{1+\sin(x)} \right) $$

What do you get after trying this?

 

[Sean1]

Thanks for getting me started.

This is my working. Can you confirm my approach is correct?

View attachment 4467

 

[Jameson]

Looks good! :)