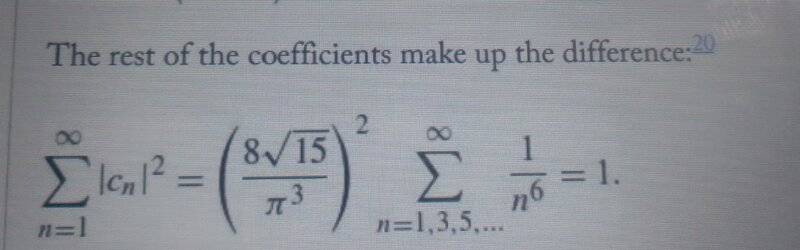- #1
phymath7
- 48
- 4
Is the infinite series ##\sum_{n=1,3,5,...}^\infty \frac {1} {n^6}## somewhat related to the Riemann zeta function?The attached image suggest the value to be inverse of the co-efficient of the series.Is there any integral representation of the series from where the series can be evaluated?