Solving 3D Statics Problem with Two Equal Mass Rods

[bigdaddynate]

I have attached a sketch of a 3-d system. There are two rods of equal length (35cm) and equal mass. The masses are equal but unknown (mass of rod #1 = mass of rod #2). Please note that rod #2 is attached to rod one by a small connecting rod (3cm in length). Also note that the width of all rods is arbitrary. The question asks to sum the moments around point O & find the reactions of each rod.

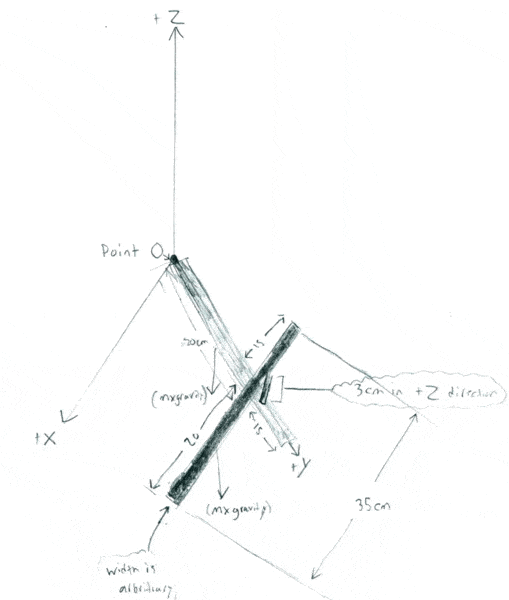
(Please click on image for a larger view)

I would really appreciate any input or advice on how to go about this problem. Thanks in advance.

 

[teknodude]

the image isn't showing up. Try uploading it to fileshack or something.

All i can say for now is draw a diagrams and label all your force. If they ask you to sum moments at a points then you will have to use the cross product or right rule.