HyperSniper
- 39
- 2
I'm pretty confused on what the difference between what the temperature reading is from a thermistor vs. the Steinhart Temperature.
Basically I know that the "Steinhart–Hart equation" is given as:
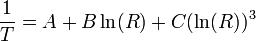
However, the http://www.vishay.com/docs/29049/23816403.pdf" for the thermistor I am using gives it's temperature value as a function of resistance as:
[PLAIN]http://img863.imageshack.us/img863/2293/unled1bo.png
Where Rref is the resistance at a reference temperature of 25 degrees C.
When I plug in my values for the resistance and the given values for A, B, and C into the "Steinhart–Hart equation" the values are far, far, too low to be correct. However the equation from the datasheet works just fine.
So what it kind of looks like to me is that to get the "Steinhart–Hart equation" to work I would have to get the coefficients from known temperatures, is that correct or am I just completely off?
Basically I know that the "Steinhart–Hart equation" is given as:
However, the http://www.vishay.com/docs/29049/23816403.pdf" for the thermistor I am using gives it's temperature value as a function of resistance as:
[PLAIN]http://img863.imageshack.us/img863/2293/unled1bo.png
Where Rref is the resistance at a reference temperature of 25 degrees C.
When I plug in my values for the resistance and the given values for A, B, and C into the "Steinhart–Hart equation" the values are far, far, too low to be correct. However the equation from the datasheet works just fine.
So what it kind of looks like to me is that to get the "Steinhart–Hart equation" to work I would have to get the coefficients from known temperatures, is that correct or am I just completely off?
Last edited by a moderator: