- #1
Eric_H
Hi all,
I was trying the understand theory behind Fourier and Laplace Transform (especially in the context of control theory) by reading the book "Complex Variables and the Laplace Transform for Engineers" written by "Wilbur R. LePage".
In section 6-10 of the book the author touches on the application of multivalued functions in root locus and said "the portion of the real axis in the neighborhood of a branch point w_o on the real axis transforms into a system of radial 'spokes', as shown in Fig. 6-15."
I am confused about the statement as I thought the transformation of the neighborhood of a branch depends on the function we are considering. For instance in the earlier examples in the book, the sq root, cubic root (and in general n-th root I believe) do forms a star / radial 'spokes'. However, in the section 6-10, the function we are converning: w = A(s)H(s) is a ratio of polynomials which I assume may have different behaviour than a simple n-th root?
Any help is appreciated.
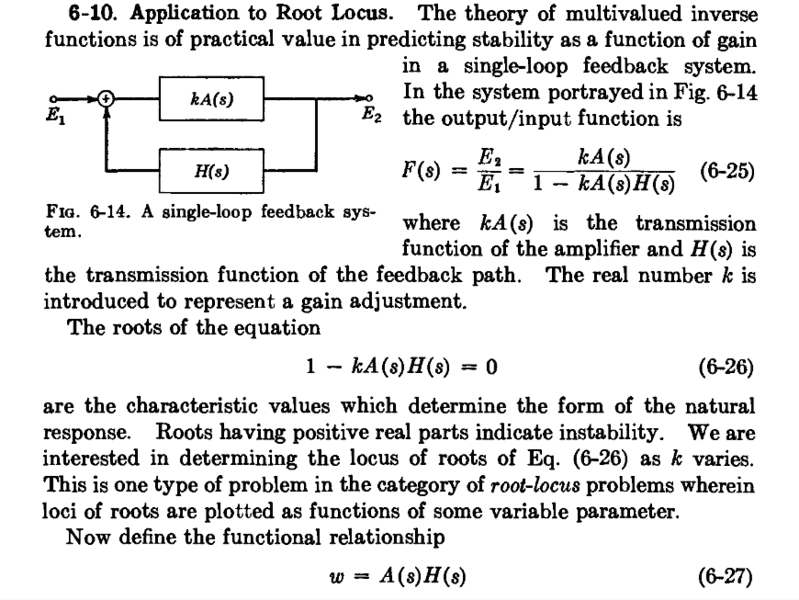

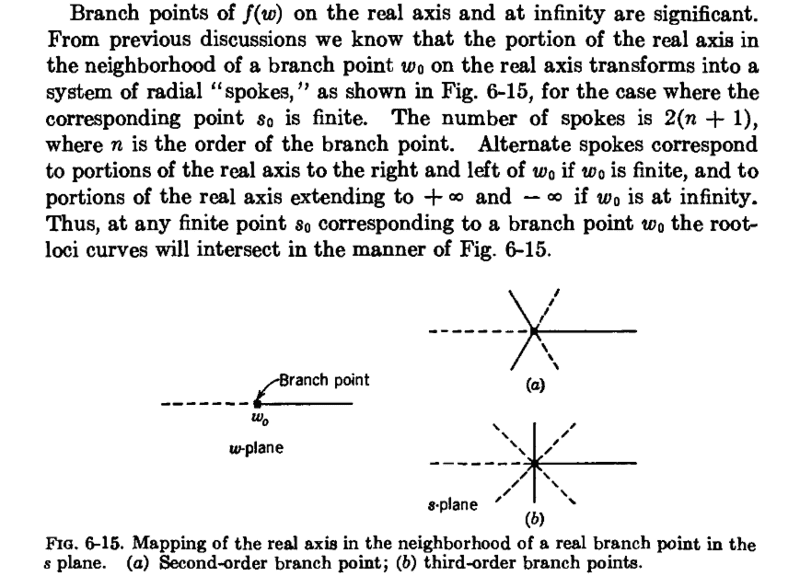
I was trying the understand theory behind Fourier and Laplace Transform (especially in the context of control theory) by reading the book "Complex Variables and the Laplace Transform for Engineers" written by "Wilbur R. LePage".
In section 6-10 of the book the author touches on the application of multivalued functions in root locus and said "the portion of the real axis in the neighborhood of a branch point w_o on the real axis transforms into a system of radial 'spokes', as shown in Fig. 6-15."
I am confused about the statement as I thought the transformation of the neighborhood of a branch depends on the function we are considering. For instance in the earlier examples in the book, the sq root, cubic root (and in general n-th root I believe) do forms a star / radial 'spokes'. However, in the section 6-10, the function we are converning: w = A(s)H(s) is a ratio of polynomials which I assume may have different behaviour than a simple n-th root?
Any help is appreciated.