Understanding Topology: Closure, Boundary & Open/Closed Sets

In summary, Andrew Browder's book "Mathematical Analysis: An Introduction" discusses topology in Chapter 6, specifically focusing on Section 6.1 about topological spaces. The author defines the boundary of a set and notes that it is empty if and only if the set is both open and closed. This may seem counterintuitive, but it is true because an open set contains none of its boundary points, while a closed set contains all of its boundary points. Browder also provides definitions for closure and a basic proposition involving closure. This clarification is helpful for understanding the concept of boundaries in sets.
  • #1
Math Amateur
Gold Member
MHB
3,990
48
I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...

I am reading Chapter 6: Topology ... ... and am currently focused on Section 6.1 Topological Spaces ...

I need some help in order to fully understand a statement by Browder in Section 6.1 ... ...


The relevant statements by Browder follow Definition 6.10 and read as follows:

View attachment 9156
View attachment 9157In the above text we read the following:

" ... ... The set \(\displaystyle \overline{E}\) \ \(\displaystyle E^{ \circ }\) is referred to as the boundary of \(\displaystyle E\), and is denoted by \(\displaystyle \text{bdry } E\); it is easy to see that \(\displaystyle \text{bdry } E = \emptyset\) if and only if \(\displaystyle E\) is both open and closed ... ... "My question is as follows:

Can someone explain and demonstrate rigorously how/why \(\displaystyle \text{bdry } E = \emptyset\) if and only if \(\displaystyle E\) is both open and closed ... ... ?
Note: I was surprised at Browder's remark above because I was always under the impression (delusion?) that an open set had an empty set as its boundary ...
Help will be appreciated ... ...

Peter======================================================================================The closure of a subset of a topological space is an important notion in the above post so I am providing Browder's definition of closure as well as a basic proposition involving closure ... as follows ...

View attachment 9158

It may help readers of the above post to have access to Browder's fundamental topological definitions ... so I am providing the same as follows ... ...

View attachment 9159
View attachment 9160
View attachment 9161Hope that helps ...

Peter
 

Attachments

  • Browder - 1 - Defn of Interior 6.10 and Relevant Remarks ... PART 1 ... ....png
    Browder - 1 - Defn of Interior 6.10 and Relevant Remarks ... PART 1 ... ....png
    11.2 KB · Views: 67
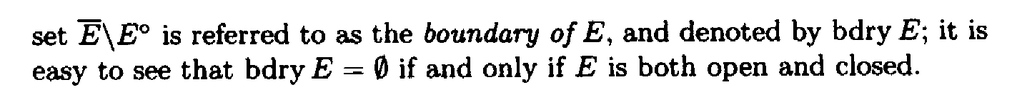  • Browder - 2 - Defn of Interior 6.10 and Relevant Remarks ... PART 2 ... .png
    Browder - 2 - Defn of Interior 6.10 and Relevant Remarks ... PART 2 ... .png
    3.7 KB · Views: 61
  • Browder - Defn of Closure 6.7 and Relevant Propn 6.8 ... .png
    Browder - Defn of Closure 6.7 and Relevant Propn 6.8 ... .png
    21 KB · Views: 66
  • Browder - 1 - Start of 6.1 - Relevant Defns & Propns ... PART 1 ... .png
    Browder - 1 - Start of 6.1 - Relevant Defns & Propns ... PART 1 ... .png
    15.4 KB · Views: 53
  • Browder - 2 - Start of 6.1 - Relevant Defns & Propns ... PART 2 ... .png
    Browder - 2 - Start of 6.1 - Relevant Defns & Propns ... PART 2 ... .png
    18.7 KB · Views: 56
  • Browder - 3 - Start of 6.1 - Relevant Defns & Propns ... PART 3 ... .png
    Browder - 3 - Start of 6.1 - Relevant Defns & Propns ... PART 3 ... .png
    56.3 KB · Views: 67
Last edited:
Physics news on Phys.org
  • #2
Note: I was surprised at Browder's remark above because I was always under the impression (delusion?) that an open set had an empty set as its boundary …​


I can't say whether you are deluded or not but you are certainly wrong! Consider the "open interval" (0, 1) in R. Its closure is the closed set [0, 1]. Its boundary is {0, 1}.

What is true of an open set is that "an open set contains none of its boundary points", not that has no boundary points.

A closed set, conversely contains all of its boundary points. A set is both "open" and "closed" if and only if "none" is the same as "all". That is, if the set has no boundary points.
​
 
  • #3
HallsofIvy said:
I can't say whether you are deluded or not but you are certainly wrong! Consider the "open interval" (0, 1) in R. Its closure is the closed set [0, 1]. Its boundary is {0, 1}.

What is true of an open set is that "an open set contains none of its boundary points", not that has no boundary points.

A closed set, conversely contains all of its boundary points. A set is both "open" and "closed" if and only if "none" is the same as "all". That is, if the set has no boundary points.
[/FONT][/COLOR][/LEFT]
Oh yes ... of course ... you're right ...

Thanks for the clarification... it was most helpful...

Peter
 

1. What is topology?

Topology is a branch of mathematics that studies the properties of space that are preserved under continuous deformations, such as stretching or bending, but not tearing or gluing. It is concerned with the study of geometric objects and their relationship to one another.

2. What is closure in topology?

In topology, closure refers to the set of all points that are either contained within a given set or are limit points of that set. It is denoted by a bar over the set, such as A̅. The closure of a set includes all of its boundary points.

3. What is the boundary of a set in topology?

The boundary of a set in topology is the set of all points that are neither contained within the set nor in its complement. It is denoted by ∂A. The boundary of a set is important because it helps define the interior and exterior of a set.

4. What is the difference between an open set and a closed set in topology?

An open set in topology is a set that does not contain any of its boundary points, while a closed set contains all of its boundary points. In other words, an open set is a set where all of its points are interior points, while a closed set includes its boundary points.

5. How are open and closed sets related to each other in topology?

In topology, a set can be both open and closed, in which case it is called a clopen set. A set can also be neither open nor closed, such as the set of all real numbers between 0 and 1. Additionally, the complement of an open set is a closed set, and vice versa.

Similar threads

MHB Neighbourhoods and Open Neighbourhoods .... Browder, Proposition 6.8 .... ....
    • Topology and Analysis
Replies
3
Views
1K
I Interior and Closure in a Topological Space .... .... remark by Willard
    • Topology and Analysis
Replies
2
Views
1K
MHB Differentials in R^n .... Remark by Brwder, Section 8.2 .... ....
    • Topology and Analysis
Replies
7
Views
2K
MHB Operator Norm .... differences between Browder and Field ....
    • Topology and Analysis
Replies
2
Views
1K
MHB Help Understanding Andrew Browder's Proposition 8.14
    • Topology and Analysis
Replies
2
Views
1K
I Differential Forms & Tensor Fiekds .... Browder, Section 13.1
    • Topology and Analysis
Replies
3
Views
2K
I The Riemann and Darboux Integrals .... Browder, Theorem 5.10 .... ....
    • Topology and Analysis
Replies
6
Views
2K
MHB The Riemann and Darboux Integrals .... Browder, Theorem 5.10 .... ....
    • Topology and Analysis
Replies
2
Views
1K
MHB Differentials in R^n .... Another Remark by Browder, Section 8.2 .... ....
    • Topology and Analysis
Replies
2
Views
1K
I On two definitions of locally compact
    • Topology and Analysis
Replies
5
Views
214

Hot Threads

Recent Insights

Back
Top