Why do we need to use causality arguments in the Landau damping problem?

[TheCanadian]

Related to Figure 8.4 the author mentions this when stating (8.25): "Note that the semi-circle deviates below the real

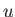-axis, rather than above, because the integral is calculated by letting the pole approach the axis from the upper half-plane in

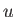-space."

Why is the pole calculated in this way? Is it a consequence of Jordan's lemma? Could the exact same problem be solved by instead approaching the axis from the bottom half-plane?

This whole process just seems a little foreign to me and I'm not quite understanding the exact reasoning behind their work as it seems like a simple task to find the residue yet it's not obvious to me whether that integral along the real line should have a semicircle above or below the axis when it encounters a pole. Based on Jordan's lemma I thought it would depend on the form of the function, F.

 

[jasonRF]

You really need to start with the basics of how Laplace transforms work.The Laplace transform $\bar{F}_1(u,p)$ is an analytic function of $p$ when the real part of $p$ is sufficiently large. That is, it is an analytic function of $p$ in a right half-plane. The Bromwich contour for the inverse Laplace transform is a vertical path in that right half-plane in which the function is analytic. It can be any vertical path inside this half-plane and the inversion contour gives the same result since the integrand is analytic (recall the deformation theorem from complex analysis). This means the path can be a vertical contour to the right of the imaginary axis ($\Re p > 0$), so for now let start with such a path.

Now recall that $\bar{F}_1(u,p)$ includes integrals of the form
$$I(p) = \int_{-\infty}^\infty \frac{G(u)}{u-ip/k}du.$$
We just said that we will invert the Laplace transform by integrating along a contour for which $p$ has a positive real part, which means the integrand of $I(p)$ has a pole at a location with a positive imaginary part.

Now consider what happens if we want to deform the Bromwich countour for the inverse Laplace transform. First of all, we cannot just willy-nilly move the contour outside of the half-plane in which $\bar{F}_1(u,p)$ is an analytic function and still get the same answer (deformation theorem only holds for analytic functions). So if we want to examine the asymptotic behavior and push the contour far to the left as in Figure 8.2 of your link, we need to analytically continue $\bar{F}_1(u,p)$ so that is analytic on the final contour and in-between the original contour and the final contour. As we push the contour far to the left as in Figure 8.2, we will have portions of the contour for which the real part of $p$ is negative. However, recall $\bar{F}_1(u,p)$ includes integrals like $I(p)$, so as we move the real part of $p$ from positive to negative $I(p)$ will be discontinuous unless we keep the pole on the same side of the contour used to calculate $I(p)$. The pole was above the contour for $\Re p >0$ so must remain above the contour for $\Re p< 0$. So as you move the Bromwich contour for the inversion of $\bar{F}_1(u,p)$ to the left you must deform the contour used for $I(p)$ as shown in 8.3 and 8.4. EDIT: in case it wasn't clear, this deformation of the contour used for calculating $I(p)$ is all that we need to do to analytically continue $\bar{F}_1(u,p)$ into the left half plane (minus the singularities).

Note that if you wanted to do a more brute-force inversion of the Laplace transform by closing the contour with a large semicircular path in the left-half-plane and using the residue theorem you can of course do so, but you still need to analytically continue $\bar{F}_1(u,p)$ into the left half-plane (minus the singularities, of course) in order to justify the added contour and for the residue theorem to apply at all. So no matter what approach you take you need to deform the contour used to calculuate $I(p)$.

It comes down to this: you cannot use the powerful theorems of complex analysis (Cauchy, residue, deformation, ...) without satisfying all of the conditions required for those theorems to hold.

EDIT: 2 things. First, when I re-read the last sentence above it sounds pretty arrogant and condescending - it is not how I intended it! Second, above I failed to explicitly point out that the right half-plane in which the Laplace transform $\bar{F}_1(u,p)$ is analytic will be to the right of all the singularities, and in this case that includes the singularities associated with $I(p)$. This fact alone means that all Bromwich contours prior to analytic continuation imply the integrand of $I(p)$ has a pole at a location with positive imaginary part.

Jason

 

[TheCanadian]

You really need to start with the basics of how Laplace transforms work.The Laplace transform $\bar{F}_1(u,p)$ is an analytic function of $p$ when the real part of $p$ is sufficiently large. That is, it is an analytic function of $p$ in a right half-plane. The Bromwich contour for the inverse Laplace transform is a vertical path in that right half-plane in which the function is analytic. It can be any vertical path inside this half-plane and the inversion contour gives the same result since the integrand is analytic (recall the deformation theorem from complex analysis). This means the path can be a vertical contour to the right of the imaginary axis ($\Re p > 0$), so for now let start with such a path.

Now recall that $\bar{F}_1(u,p)$ includes integrals of the form
$$I(p) = \int_{-\infty}^\infty \frac{G(u)}{u-ip/k}du.$$
We just said that we will invert the Laplace transform by integrating along a contour for which $p$ has a positive real part, which means the integrand of $I(p)$ has a pole at a location with a positive imaginary part.

Now consider what happens if we want to deform the Bromwich countour for the inverse Laplace transform. First of all, we cannot just willy-nilly move the contour outside of the half-plane in which $\bar{F}_1(u,p)$ is an analytic function and still get the same answer (deformation theorem only holds for analytic functions). So if we want to examine the asymptotic behavior and push the contour far to the left as in Figure 8.2 of your link, we need to analytically continue $\bar{F}_1(u,p)$ so that is analytic on the final contour and in-between the original contour and the final contour. As we push the contour far to the left as in Figure 8.2, we will have portions of the contour for which the real part of $p$ is negative. However, recall $\bar{F}_1(u,p)$ includes integrals like $I(p)$, so as we move the real part of $p$ from positive to negative $I(p)$ will be discontinuous unless we keep the pole on the same side of the contour used to calculate $I(p)$. The pole was above the contour for $\Re p >0$ so must remain above the contour for $\Re p< 0$. So as you move the Bromwich contour for the inversion of $\bar{F}_1(u,p)$ to the left you must deform the contour used for $I(p)$ as shown in 8.3 and 8.4. EDIT: in case it wasn't clear, this deformation of the contour used for calculating $I(p)$ is all that we need to do to analytically continue $\bar{F}_1(u,p)$ into the left half plane (minus the singularities).

Note that if you wanted to do a more brute-force inversion of the Laplace transform by closing the contour with a large semicircular path in the left-half-plane and using the residue theorem you can of course do so, but you still need to analytically continue $\bar{F}_1(u,p)$ into the left half-plane (minus the singularities, of course) in order to justify the added contour and for the residue theorem to apply at all. So no matter what approach you take you need to deform the contour used to calculuate $I(p)$.

It comes down to this: you cannot use the powerful theorems of complex analysis (Cauchy, residue, deformation, ...) without satisfying all of the conditions required for those theorems to hold.

EDIT: 2 things. First, when I re-read the last sentence above it sounds pretty arrogant and condescending - it is not how I intended it! Second, above I failed to explicitly point out that the right half-plane in which the Laplace transform $\bar{F}_1(u,p)$ is analytic will be to the right of all the singularities, and in this case that includes the singularities associated with $I(p)$. This fact alone means that all Bromwich contours prior to analytic continuation imply the integrand of $I(p)$ has a pole at a location with positive imaginary part.

Jason

Thank you greatly for that explanation! I've studied the concepts but perhaps am struggling to connect a few of the bigger pieces together. Your words certainly helped (and I am re-reading it), but perhaps to make the point clear in my head and correct any other misconceptions of mine, I should present an example of contour integration without Laplace transforms that's been puzzling me a little.

Let's perform the following integral:

$\chi = \frac {q^2}{\omega m \epsilon_0} \int_{-\infty}^\infty \frac {v \frac{\partial f } {\partial v} } { \omega - kv } dv$

where $k$ is real, $\omega$ is complex, and $v$ is complex. As displayed above, the integral is to be taken along the real axis in velocity.

Case 1) $\Im \omega > 0$, which implies the pole is above the real axis

Case 2) $\Im \omega = 0$, which implies the pole is on the real axis

Case 3) $\Im \omega < 0$, which implies the pole is below the real axis

I was told that for case 1 there is no difficulty about the integration because the pole is above the real axis. Yet for cases 2 and 3, I was told analytic continuation is required and that the contour must be continuously deformed as the pole ($v = \omega/k$) is shifted down the imaginary axis (in velocity space) and that we must integrate below the pole.

I suppose I just never understood in this case why the integration must be carried out below the pole. Why not above the pole? What about the form of the integrand ($f$ is likely a Maxwellian distribution) and the pole necessitates one to integrate below the pole and thus able to neglect the pole altogether when $\Im \omega > 0$ yet not $\Im \omega \leq 0$?

 

[jasonRF]

The entire issue is that the integral you are looking at is inside an inverse Laplace transform integral so thinking about it in isolation is not helpful here. So let me examine a simplified problem that has the essential features of the Landau damping problem. First consider the inverse Laplace transform with the original contour in the region of analyticity:
$f(t) = \frac{1}{2\pi i}\int_{\gamma_0} e^{p t} \left(\int_{-\infty}^{\infty} \frac{G(u)}{u-ip/k}du \right) dp = \frac{1}{2\pi i}\int_{\gamma_0} e^{p t} I(p) dp$
where $\gamma_0$ is a vertical contour in the region where the Laplace transform is analytic (shown in Figure 8.1 of the notes). This region is to the right of all singularities, so allong $\gamma_0$ the real part of $p$ will be positive. In this regime, we evaluate $I(p)=\int_{-\infty}^{\infty} \frac{G(u)}{u-ip/k}du$ by integrating along the real axis, and the pole is located at a point that has a positive imaginary part.Now, we would like to deform the inverse Laplace transform contour $\gamma_0$ by pushing it to the left so that portions of it will be to the left of the imaginary axis (that is, will have negative real part); let this new contour be $\gamma_1$. Figure 8.2 of the notes shows a picture of $\gamma_1$. However,if we just consider $I(p)=\int_{-\infty}^{\infty} \frac{G(u)}{u-ip/k}du$ to be an integral along the real axis it is discontinuous and hence not analytic: there is a jump where the real part of $p$ is zero. This means we cannot deform the $\gamma_0$ contour to $\gamma_1$ like we would want. The solution of our problem is to define a new function $I_1(p)=\int_\beta \frac{G(u)}{u-ip/k}du$ where $\beta$ is the contour shown in Figures 8.3 and 8.4 of the notes. Note that $I_1(p)=I(p)$ when the real part of $p$ is positive, but $I_1(p)$ does not have the discontinuity that $I(p)$ does. This new function, $I_1(p)$, is the analytic continuation of $I(p)$ into a larger region of the complex plane. Note that with our original Laplace inversion contour,
$f(t) =\frac{1}{2\pi i}\int_{\gamma_0} e^{p t} I(p) dp = \frac{1}{2\pi i}\int_{\gamma_0} e^{p t} I_1(p) dp$.
But now we are allowed to deform $\gamma_0$ to be $\gamma_1$ since $I_1(p)$ is analytic on $\gamma_1$ and between $\gamma_0$ and $\gamma_1$. Indeed,
$f(t) =\frac{1}{2\pi i}\int_{\gamma_0} e^{p t} I(p) dp = \frac{1}{2\pi i}\int_{\gamma_0} e^{p t} I_1(p) dp = \frac{1}{2\pi i}\int_{\gamma_1} e^{p t} I_1(p) dp$.
The last integral has the advantage that it is easy to approximate for large $t$.

Did that help?

Jason

 

[TheCanadian]

The entire issue is that the integral you are looking at is inside an inverse Laplace transform integral so thinking about it in isolation is not helpful here.

With regards to considering the integral in isolation, the attached set of notes does this in equation (5.213). It is only afterwards that they utilize Laplace transforms, which is why I proposed this alternate question. Although maybe details are omitted.

Now, we would like to deform the inverse Laplace transform contour γ0γ0\gamma_0 by pushing it to the left so that portions of it will be to the left of the imaginary axis (that is, will have negative real part); let this new contour be γ1γ1\gamma_1. Figure 8.2 of the notes shows a picture of γ1γ1\gamma_1.

Is there a particular reason for wanting to push the contour to the left of the imaginary axis? I understand the process of what was done now (thank you for the explanation), but am not quite seeing the motivation behind why it's desirable in the first place. Is it simply because we want values of p (i.e. the wave frequency) to be unrestricted in its real or imaginary components?

Figure 8.2 of the notes shows a picture of γ1γ1\gamma_1. However,if we just consider I(p)=∫∞−∞G(u)u−ip/kduI(p)=∫−∞∞G(u)u−ip/kduI(p)=\int_{-\infty}^{\infty} \frac{G(u)}{u-ip/k}du to be an integral along the real axis it is discontinuous and hence not analytic: there is a jump where the real part of ppp is zero. This means we cannot deform the γ0γ0\gamma_0 contour to γ1γ1\gamma_1 like we would want.

To clarify a simple point: gamma is a vertical line running parallel to the imaginary axis and not a closed contour (e.g. semicircle going out to infinity), correct? Okay, now that is clear to me that in Fig 8.2 that the real part of p can be 0 and thus the integral diverges, so we must avoid this.

The solution of our problem is to define a new function $I_1(p)=\int_\beta \frac{G(u)}{u-ip/k}du$ where $\beta$ is the contour shown in Figures 8.3 and 8.4 of the notes. Note that $I_1(p)=I(p)$ when the real part of $p$ is positive

I agree. And it appears that if the pole is initially above the real v axis, if the pole is then moved downward in imaginary v space, since the integral is running from $-\infty$ to $+\infty$ the contour is deformed as shown strictly below the pole. That much makes sense to me and hopefully my interpretation is correct. But if the pole is initially below the real v axis, and is now instead moved upwards in imaginary v space, when the contour is deformed wouldn't it be above the pole?

Thank you again for all the help, it's certainly been insightful and I think I'm close to grasping the essential parts of this topic.

 

[jasonRF]

Is there a particular reason for wanting to push the contour to the left of the imaginary axis? I understand the process of what was done now (thank you for the explanation), but am not quite seeing the motivation behind why it's desirable in the first place.

I recall being initiall puzzled by it as well - it made sense but was not what I would have done. If it were me, I would do the standard thing of appending a semicircular contour (closed to the left) to the initial vertical contour, show that the contribution due to the circular contour is zero in the limit of infinite radius, then use the residue theorem. Of course, the residue theorem only applies if the integrand is analytic everywhere on the contour, and everywhere inside the contour except for isolated singularities. So we still need to do the analytic continuation in order to apply the residue theorem. The contribution from the residue at the right-most pole would then dominate the solution for large time.

Of course, if it were me I also would have missed the fact that the integrand was not analytic and ended up with the wrong result. I had taken a solid complex analysis class from the math department, but my skills weren't quite up to the standard needed for this when I saw it my first semester of graduate school. After completing my graduate work in plasma physics I had a much stronger understanding of complex analysis and integral transforms, which occasionally comes in handy even though I no longer do plasma physics.

I don't know what Landau's motivation was, but I have certainly seen some authors that regularly deform an initial contour instead of appending an extra semicircle (or other shaped contour) to the original problem. Nearing does this in his undergrad math methods book:
http://www.physics.miami.edu/~nearing/mathmethods/
To me it appears that Landau is essentially using this approach.

To clarify a simple point: gamma is a vertical line running parallel to the imaginary axis and not a closed contour (e.g. semicircle going out to infinity), correct? Okay, now that is clear to me that in Fig 8.2 that the real part of p can be 0 and thus the integral diverges, so we must avoid this.

Yes. The basic inversion theorem for Laplace transforms tells us that the contour $\gamma_0$ is a vertical line parallel to the imaginary axis. The version I learned is this: if $f(t)$ is piecewise smooth on $[0,\infty)$ and $F(s)=\int_{0}^{\infty} e^{-s t} f(t) \, dt$ is analytic for $\Re s > \sigma_0$, then,
$\frac{1}{2}\left(f(t+0) + f(t-0)\right) = \lim_{R \rightarrow \infty} \frac{1}{2\pi i} \int_{\sigma - iR}^{\sigma + iR} e^{st} F(s) \, ds$
for any $\sigma > \sigma_0$. The left hand side simply says that if $f$ is discontinuous at $t$, then the inversion will give the average value across that discontinuity. The right-hand side makes it explicitly clear that the principal value integral provides the inversion, which is very nice because most of our contour integral tricks we would like to do (including the "adding the semicircle" trick above) yields a principal value integral. Of course, once you have this contour you can deform it at will as long as the deformation does not cross any singularities.

But if the pole is initially below the real v axis, and is now instead moved upwards in imaginary v space, when the contour is deformed wouldn't it be above the pole?

yes, but that is not the case we have.

 

[TheCanadian]

Thank you for all the help!

That integral trick finally clears up where the principal value I keep finding is derived from. I was looking at (8.25) and (8.26) from the first link and wondering where the principal value arises from since it appeared to be an integration strictly below the pole (and thus not an average above and below), but your comment helps demystify that.

yes, but that is not the case we have.

But if it was the case, would the contour run above the pole? I have searched multiple derivations and they all essentially do the same thing where the contour is taken below the pole. Perhaps they are all copying Landau's original approach, but they never explain why they start above the real axis and move downwards (i.e. $\Im \omega > 0$), they simply state that as a given. As opposed to the opposite situation of starting below the axis and moving upwards (i.e. $\Im \omega < 0$), which I haven't seen in the literature for reasons unknown to me.

 

[jasonRF]

That integral trick finally clears up where the principal value I keep finding is derived from. I was looking at (8.25) and (8.26) from the first link and wondering where the principal value arises from since it appeared to be an integration strictly below the pole (and thus not an average above and below), but your comment helps demystify that.

Those principal values are different - specifically for 8.25 they are looking at the case where $\omega$ is real, so
$P \int_{-\infty}^{\infty} \frac{\partial F_0 / \partial u}{\omega-ku}du = \lim_{\epsilon \rightarrow 0^+} \left[ \int_{-\infty}^{\omega/k-\epsilon} \frac{\partial F_0 / \partial u}{\omega-ku}du +\int_{\omega/k+\epsilon}^{\infty} \frac{\partial F_0 / \partial u}{\omega-ku}du \right]$
This comes from taking the limit of the contour in Figure 8.4 as the pole approaches the real axis.

But if it was the case, would the contour run above the pole? I have searched multiple derivations and they all essentially do the same thing where the contour is taken below the pole. Perhaps they are all copying Landau's original approach, but they never explain why they start above the real axis and move downwards (i.e. $\Im \omega > 0$), they simply state that as a given. As opposed to the opposite situation of starting below the axis and moving upwards (i.e. $\Im \omega < 0$), which I haven't seen in the literature for reasons unknown to me.

The region in which the Laplace transform is analytic (and hence defined at all prior to any analytic continuation) has $\Re p > 0$. When $\Re p >0$ integrals of the form $I(p) = \int_{-\infty}^{\infty} \frac{G(u)}{u-ip/k}du$ (where $k=|\mathbf{k}|$ is non-negative) have a pole in the upper half-plane. When we do the inversion contour integral along $\gamma_0$, all of the values of $p$ on that contour have positive real part. That is why they always start with the pole in the upper half-plane; it is not an arbitrary decision.

 

[TheCanadian]

Those principal values are different - specifically for 8.25 they are looking at the case where ωω\omega is real, so
P∫∞−∞∂F0/∂uω−kudu=limϵ→0+[∫−ϵ−∞∂F0/∂uω−kudu+∫∞ϵ∂F0/∂uω−kudu]P∫−∞∞∂F0/∂uω−kudu=limϵ→0+[∫−∞−ϵ∂F0/∂uω−kudu+∫ϵ∞∂F0/∂uω−kudu] P \int_{-\infty}^{\infty} \frac{\partial F_0 / \partial u}{\omega-ku}du = \lim_{\epsilon \rightarrow 0^+} \left[ \int_{-\infty}^{-\epsilon} \frac{\partial F_0 / \partial u}{\omega-ku}du +\int_{\epsilon}^{\infty} \frac{\partial F_0 / \partial u}{\omega-ku}du \right]
This comes from taking the limit of the contour in Figure 8.4 as the pole approaches the real axis.

Of course! Thank you for the clarification.

The region in which the Laplace transform is analytic (and hence defined at all prior to any analytic continuation) has Rp>0ℜp>0\Re p > 0. When Rp>0ℜp>0\Re p >0 integrals of the form I(p)=∫∞−∞G(u)u−ip/kduI(p)=∫−∞∞G(u)u−ip/kduI(p) = \int_{-\infty}^{\infty} \frac{G(u)}{u-ip/k}du (where k=|k|k=|k|k=|\mathbf{k}| is non-negative) have a pole in the upper half-plane. When we do the inversion contour integral along γ0γ0\gamma_0, all of the values of ppp on that contour have positive real part. That is why they always start with the pole in the upper half-plane; it is not an arbitrary decision.

Yes, when taking the Laplace transform we require $\Re p>0$ and thus the pole exists in the upper half plane. I understand the individual steps involved if we perform the Laplace transform (and the resulting restrictions on how we can deform the contour), but am just failing to see why the simple integral of $\frac {q^2}{\omega m \epsilon_0} \int_{-\infty}^\infty \frac {v \frac{\partial f } {\partial v} } { \omega - kv } dv$ cannot be solved without a Laplace transform in the first place (where if the pole is on the real line, we can use an alternative approach of integrating over a semicircle and including poles via reside theorem). I believe you mention it's because the integrand is not analytic, but that is only in the neighbourhood of the pole.

 

[jasonRF]

Yes, when taking the Laplace transform we require $\Re p>0$ and thus the pole exists in the upper half plane. I understand the individual steps involved if we perform the Laplace transform (and the resulting restrictions on how we can deform the contour), but am just failing to see why the simple integral of $\frac {q^2}{\omega m \epsilon_0} \int_{-\infty}^\infty \frac {v \frac{\partial f } {\partial v} } { \omega - kv } dv$ cannot be solved without a Laplace transform in the first place (where if the pole is on the real line, we can use an alternative approach of integrating over a semicircle and including poles via reside theorem). I believe you mention it's because the integrand is not analytic, but that is only in the neighbourhood of the pole.

I don't see why you care about this integral at all outside the context of this problem. For our problem, the integral arises in a scenario with the pole is in the upper half plane and that is part of specifying what the integral means.

If for some reason you want to throw away the physics of the problem and consider the integral in a vacuum then you are free to do so. It is undefined when the pole is on the real axis, and in this case the integral as written is meaningless. If the pole is either below or above the real axis we are free to keep the integral along the real axis with no dents if we want (after all, it is an integral considered in a vacuum without any extra information attached). Of course you are no longer solving the Landau damping problem, but simply doing some math for an arbitrary reason. Nothing wrong with that, but I have been thinking that you are trying to understand the Landau damping problem.

As I stated above, the integral as written is not defined when the pole is on the real axis - there is nothing to `solve' in this case. You might try limiting cases by considering
$I(y) = \int_{-\infty}^\infty \frac{G(u)}{u - (x+i y)}du.$
This function is well defined for $y>0$ and $y<0$, but is undefined at $y=0$. We can analyze the limiting cases by denting contours and taking limits, for which I get
$\lim_{y\rightarrow 0^+} I(y) = P \int_{-\infty}^\infty \frac{G(u)}{u - x}du + i \pi G(x).$
$\lim_{y\rightarrow 0^-} I(y) = P \int_{-\infty}^\infty \frac{G(u)}{u - x}du - i \pi G(x).$
This just illustrates that $I(y)$ is discontinuous at the origin. So you have a discontinuous function that is defined on both sides of the discontinuity but not at the point of discontinuity, and you are trying to assign that function a particular value there. Essentially you can arbitrarily define $I(0)$ to be whatever you want it to be because you are doing math in a vacuum with no physical meaning, but it is completely arbitrary unless you have a reason to prefer one definition over any other. For the Landau damping problem we indeed do have a reason to prefer a particular limit because it has physical meaning.

Edit:I should add that the resolution of this ambiguity of how to treat the singularity by using the Laplace transform to analyze the initial value problem (as opposed to using simple phasor analysis which assumes $e^{-i \omega t}$ behavior) is is an important (perhaps the most important) contribution of Landau's work. That is the big idea behind this entire analysis.

Jason

 

[jasonRF]

A couple more comments to clear up what may be some confusion on your point:

... failing to see why the simple integral of $\frac {q^2}{\omega m \epsilon_0} \int_{-\infty}^\infty \frac {v \frac{\partial f } {\partial v} } { \omega - kv } dv$ cannot be solved without a Laplace transform in the first place (where if the pole is on the real line, we can use an alternative approach of integrating over a semicircle and including poles via reside theorem).

First, the `simple' integral arose from a Laplace transform analysis - we are not using the laplace transform to solve this integral. We are simply using the knowledge we have about where the Laplace transform is defined to properly analyze the problem and obtain a physically meaningful result.

Second, the integral is not over a closed contour, so even if it were defined when the pole is on the real axis I don't know how you are using the residue theorem. I certainly didn't use the residue theorem anywhere in my previous post.

jason

 

[TheCanadian]

I don't see why you care about this integral at all outside the context of this problem. For our problem, the integral arises in a scenario with the pole is in the upper half plane and that is part of specifying what the integral means.

I care about this integral as that is what is presented in the notes I attached above in equation (5.208). In the notes, they do not apply Laplace transforms until afterwards. This is why I think it is as simple as doing the math in a vacuum. Although I now see that in the notes that this integral is only valid for $\Im \omega > 0$, otherwise there will be an additional complementary function present (i.e. a transient). And thus as you've been writing and mentioned in the literature, we must deform the contour to go below the pole if it is going down to 0 or negative in the imaginary axis.

Returning to the first link I posted above, essentially my question boils down to what's stopping us from simply integrating (8.9)? At this point, before Laplace transforms are introduced, aren't $\omega$ and $v$ still complex-valued? In that case, sure, we know there is a pole at $\omega = \vec {k} \cdot \vec {v}$, but aside from that particular point, our integration along the real line would go unimpeded unless $\Im \omega = 0$. (I was just saying that one way to do this would be to apply Jordan's lemma and account for any poles via residue theorem, but I see now that the integrand considered does not satisfy the constraints on Jordan's lemma.)

I am just failing to see why we have to treat this as an initial value problem and can't solve the above integral (8.9). If a Laplace transform is applied and we follow the prescription, all the steps make sense to me (thank you for that). But why must we treat this as an initial value problem and perform this transform in the first place? Is there no other way to get around it? Based on everything above, it seems the answer is because the equation (8.9) is itself incorrect as it assumed the perturbed distribution function has the form $\exp (i \omega t)$ despite there not being oscillatory behaviour for all time. I think that answers my question and clears up my confusion. The main issue I was having with the first link was the sentence: "However, in doing so, we run up against a serious problem, because the integral has a singularity in velocity space, where

, and is, therefore, not properly defined." I just kept thinking that there were ways to go about solving the integral, but that solving that integral in (8.9) isn't what we actually want to find as it assumes a form of the solution that is incorrect.

 

[jasonRF]

I care about this integral as that is what is presented in the notes I attached above in equation (5.208). In the notes, they do not apply Laplace transforms until afterwards. This is why I think it is as simple as doing the math in a vacuum. Although I now see that in the notes that this integral is only valid for $\Im \omega > 0$, otherwise there will be an additional complementary function present (i.e. a transient). And thus as you've been writing and mentioned in the literature, we must deform the contour to go below the pole if it is going down to 0 or negative in the imaginary axis.

I just spent a few minutes skimming the notes. They are appealing to causality arguments when evaluating the integral. This is a physical argument, based on a reasonable expectation that a plasma is a causal system. They are not looking at the integral purely mathematically in a vacuum, because the pure math way is ambiguous. So this is one way to get around the ambiguity without doing the initial value problem. There may be other ways, too, but in all cases the integrals will be considered in a context that makes sense physically.

Returning to the first link I posted above, essentially my question boils down to what's stopping us from simply integrating (8.9)? At this point, before Laplace transforms are introduced, aren't $\omega$ and $v$ still complex-valued? In that case, sure, we know there is a pole at $\omega = \vec {k} \cdot \vec {v}$, but aside from that particular point, our integration along the real line would go unimpeded unless $\Im \omega = 0$. (I was just saying that one way to do this would be to apply Jordan's lemma and account for any poles via residue theorem, but I see now that the integrand considered does not satisfy the constraints on Jordan's lemma.)

Why would you expect $v$ to be complex valued from the get-go? It is a physical velocity, and the velocity integral is simply in Poisson's equation in the original differential-integral equation formulation.

Yes, you can try to tackle 8.9 directly. I don't know why you would, since even the notes themselves indicate that it is not properly defined. Landau was resolving that ambiguity with the initial value approach, and the notes use how 8.9 is not well defined to motivate why you want to try another approach.

(I was just saying that one way to do this would be to apply Jordan's lemma and account for any poles via residue theorem, but I see now that the integrand considered does not satisfy the constraints on Jordan's lemma.)

Yep. Functions that look like $e^{-u^2}$ aren't very nice as the imaginary part of $u$ gets very large (either positive or negative).

I am just failing to see why we have to treat this as an initial value problem and can't solve the above integral (8.9). If a Laplace transform is applied and we follow the prescription, all the steps make sense to me (thank you for that). But why must we treat this as an initial value problem and perform this transform in the first place? Is there no other way to get around it?

The causality argument used in the notes you attached are one such way to do it without doing the initial value problem. I had actually seen that approach many years ago while in school but had forgotten it. There may be other ways as well. But the "standard" way is to solve the initial value problem, and is the only way I remembered.

Based on everything above, it seems the answer is because the equation (8.9) is itself incorrect as it assumed the perturbed distribution function has the form $\exp (i \omega t)$ despite there not being oscillatory behaviour for all time. I think that answers my question and clears up my confusion.

The problem is that there is physical information that is not being used so the equation is mathematically ill defined. It has nothing to do with the assumed dependence, which usually allows $\omega$ to be complex so is not necessarily oscillatory. Indeed, the Landau damping problem is solving for the imaginary parts of the frequencies of modes of the plasma.

The main issue I was having with the first link was the sentence: "However, in doing so, we run up against a serious problem, because the integral has a singularity in velocity space, where View attachment 220061 , and is, therefore, not properly defined." I just kept thinking that there were ways to go about solving the integral, but that solving that integral in (8.9) isn't what we actually want to find as it assumes a form of the solution that is incorrect.

Yes, the integral 8.9 is not what we want to solve. Not because of the assumed dependence, but because it is undefined for a regime we really care about. You need to find a way to make a physically meaningful definition: we now know two ways - the initial value problem and by using causality arguments. There may be other ways, too.

By the way, the same kinds of causality arguments can be used in other situations as well. For example, when solving the inhomogeneous undamped wave equation with Fourier transforms: you get poles on the real axis and correctly choosing how to dent the contour leads to a causal solution. Another way to get the correct solution is to add damping to the problem, set up the integral, then take the limit as damping goes to zero which forces you to dent the contour correctly around both poles. But in this case the causality argument is much easier to apply (at least for me) than in the Landau damping case.