Below is a description of the basic experimental settings. All participants interested in the discussion, and in particular stevendaryl, are invited to comment on the suitability of the setting to contain both experiments that display fully classical and fully quantum behavior representative of certain experiment discussing long-distance nonlocality in Bell's sense. In addition, many other experiments match the setting, e.g., those to check that the devices work individually as prescribed, by sending signals only to one of the devices.
Improvements were made to the original setting to accommodate valid criticism discussed in posts #3-#48 below. Since the basic setting is now stable, it is no longer open for discussion. If you want to go immediately to stage 2, you may continue with post #49, where I introduce additional features that impose more structure, again asking for your participation to make everything as clear and constructive as possible.
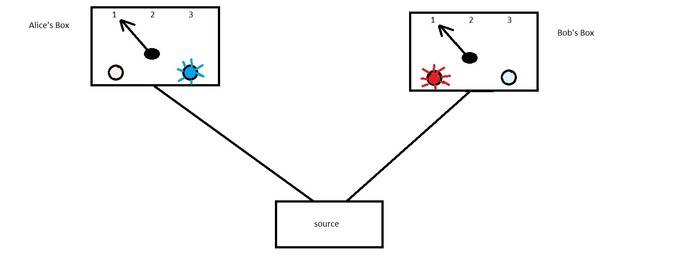
The basic setting
1. A source operated by Norbert sends a sequence of independent, identically distributed signals with temporal spacing ##\gg\delta t## but ##\ll\Delta t## seconds to two identically built devices operated by Alice and Bob, located symmetrically more than 1km apart from each other and from Norbert. (Here ##0\ll\delta t\ll\Delta t## are fixed real numbers, ##\delta t\le 2.99 \mu s##, less than the time needed to travel 1km.)
2. Each device has a pointer that can take 3 values and a red and blue light that can possibly light up for a time interval ##\ll\delta t## when a signal arrives - if this happens, this is called an event.
3. Alice and Bob randomly, uniformly, and independently change their pointer settings every ##\Delta t## seconds. Both keep a record of the time and the pointer setting of any event on their side, together with the color of the light observed. Both purify their record by omitting all events where two lights light up on their own detector within a time interval of ##\delta t##. They also discards events within ##\delta t## of their own pointer switch. The remaining events are called pure events.
4. After Alice and Bob independently collected their data for ##\gg\Delta t## seconds, each calculates a ##2\times 3## matrix ##A## respectively ##B## of statistical observables whose entries are the relative frequency ##X_{is}## of pure events where ##c_X=i,p_X=s## (##X=A,B##). They send their ##2\times 3## matrices to you, the analyzer. In addition, they send their raw data to Yvonne who evaluates their data according to the following protocol for creating the statistics.
5. Yvonne postselects events in the raw data received from Alice and Bob by discarding events when their total number within a time interval of ##\delta t## is different from 2, or equals 2 but are both on the side of Alice or of Bob. She also discards events within ##\delta t## of a pointer switch. As a consequence, all remaining events are pure and occur in pairs consisting of one event ##A## on the side of Alice and one event ##B## on the side of Bob, and to each event there are well-defined pointer settings ##p_A,p_B## of the devices of Alice and Bob. Alice and Bob characterize each event through the numbers ##c_A,c_B## defined by ##c_X:=## 1 if ##X## is red, 2 if ##X## is blue.
6. Yvonne summarizes the experiment of Alice and Bob by calculating two ##2\times 2## matrices ##E## and ##F## of statistical observables whose entries are the relative frequency ##E_{ik}## of pairs where ##c_A=i,~c_B=k,~p_A=p_B## and the relative frequency ##F_{ik}## of pairs where ##c_A=i,~c_B=k,~p_A\ne p_B##. In addition, Yvonne checks whether the total number of discarded events is within 10% of the total number of remaining events. She sends the matrices ##E,F## to you, the analyzer if this is the case; otherwise she reports to you failure of the experiment due to lack of care in the setup.
7. Other ways of analyzing the full experimental record (i.e., before postselection) are acceptable for discussing auxiliary purposes such as checking the efficiency of transmission and detection. However, the sole goal of the experiment is to study the correlations expressed in the matrices ##A,B,E,F##.
8. Alice and Bob perform their experiments synchronous with Norbert's signals, accounting for the delay due to transmission. The devices are shielded from other external influences to the extent current technology allows it. The analysis will have to make allowance for corresponding imperfections.
9. Norbert, Alice, Bob, and Yvonne are not human beings but simply acronyms for elementary control programs behind the automatized source control, detector controls, and postselection control, respectively. In particular, they are assumed not have any artificial intelligence, hence they have neither knowledge nor a capability for being surprised.
10. Some time after the whole experiment is over, you, the analyst of the experiment read Yvonne's report of the experimental data including the four matrices with the summary statistics. After checking that no mistake has been made you publish the four matrices ##A,B,E,F## in a scientific journal. (Possibly you post in addition refined statistics on a web supplement.) You and the readers of the journal are the ones who have knowledge and therefore may or may not be surprised about the published findings, depending on your world view.
The matrices ##A,B,E,F## are the published output of the experiment. They (and potentially more) are to be predicted by various existing or hypothetical theories for how certain specific signals sent by Norbert may affect the observation devices.