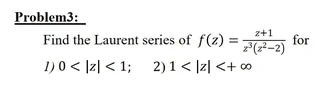SUMMARY
The discussion centers on the validity of a problem involving the Laurent series for the function \( f(z) = \frac{z+1}{z^3(z^2-2)} \). Participants express skepticism about the specified domains for the series expansions, particularly questioning the convergence for \( 1 < |z| < +\infty \) due to the presence of a pole at \( z = \sqrt{2} \). The correct domains for convergence are identified as \( 0 < |z| < \sqrt{2} \) and \( \sqrt{2} < |z| < +\infty \). The discussion emphasizes the importance of partial fraction decomposition and the correct application of series expansions.
PREREQUISITES
- Understanding of Laurent series and their convergence properties
- Familiarity with partial fraction decomposition techniques
- Knowledge of complex analysis, particularly regarding analytic functions
- Proficiency in using LaTeX for mathematical expressions
NEXT STEPS
- Study the properties of Laurent series and their convergence criteria
- Learn about partial fraction decomposition in complex functions
- Explore the implications of poles and singularities in complex analysis
- Practice writing mathematical expressions in LaTeX for clarity in communication
USEFUL FOR
Students and professionals in mathematics, particularly those focusing on complex analysis, as well as educators seeking to clarify concepts related to Laurent series and their applications.