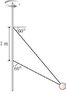
SUMMARY
The discussion focuses on solving a physics problem involving a 2.0 kg sphere revolving in a horizontal circle, specifically determining the speed at which the tension is equal in two wires attached to it. The solution involves analyzing vertical and horizontal forces, leading to the equations for tension and angular velocity. Key steps include finding the vertical force in terms of tension, writing the horizontal force equation, and calculating the radius of the circle based on wire lengths.
PREREQUISITES
- Understanding of Newton's laws of motion
- Familiarity with circular motion concepts
- Knowledge of tension in physics
- Ability to manipulate equations involving angular velocity and radius
NEXT STEPS
- Study the principles of circular motion and centripetal force
- Learn how to derive equations for tension in multiple wire systems
- Explore the relationship between angular velocity and radius in circular motion
- Practice solving problems involving forces in equilibrium
USEFUL FOR
Students studying physics, particularly those focusing on mechanics, as well as educators looking for problem-solving strategies related to tension and circular motion.