How to derive beta function as pochhammer contour integral?

[jackmell]

Hi,

We have:

\beta(a,b)=\int_0^1 t^{a-1}(1-t)^{b-1}dt,\quad Re(a)>0, Re(b)>0

and according to Wikipedia:

http://en.wikipedia.org/wiki/Pochhammer_contour

we can write:

\left(1-e^{2\pi ia}\right)\left(1-e^{2\pi ib}\right)\beta(a,b)= \int_P t^{a-1}(1-t)^{b-1}dt

valid for all a and b where P is the pochhammer contour given in the Wikipedia reference.I cannot find any type of derivation for this expression on the net. Would someone know how this is derived?Ok thanks,
Jack

 

[fzero]

Deform the contour so that it is composed of 8 parts: 2 lines from $0\rightarrow 1$, 2 lines from $1\rightarrow 0$, 2 circles of opp. orientation around each of $z=0,1$. The contribution from the arcs vanish as $R^\epsilon$ as we take the radii $R\rightarrow 0$. The 4 contributions from the lines involve appropriate choices of branches, which should very plausibly factor in the way suggested by that expression. I haven't tried to work out the details, but each term involves an additional factor of $e^{2\pi i p}$ as we wind around one of the zeros.

 

[jackmell]

Ok. Thanks a lot for that analysis fzero. Took some time but I think I barely understand it enough to summarize what I think it is. If you have time to review it, let me know if it's right.

Here's the Pochhammer plot and the homologous contour you described above:

http://img191.imageshack.us/img191/1373/zr2z.jpg

I begin the integration on the blue segment which I will place over the principal branch of the function in which case we can write in the limit as the indentations go to zero:

\mathop\int\limits_{\text{blue}} f dz=\int_0^1 f(x)dx

We then continue around the contour along the indicated path and I obtain:

\mathop\int\limits_{\text{blue}} + \mathop\int\limits_{\text{purple}}+ \mathop\int\limits_{\text{red}}+\mathop\int\limits_{\text{green}}

and as we go around the intented contours, the function values can change by either e^{\pm 2n\pi i a} or e^{\pm 2n\pi i b} so that if I carefully choose the branches I integrate over, really at this point just contrive it to get it to work, we accumulate factors of e^{2n\pi i a} or e^{2n\pi i b} and so can write the integrals as:

\int_0^1 f+e^{2\pi i b} \int_1^0 f+e^{2\pi ia}e^{2\pi ib} \int_0^1+e^{2\pi i a}e^{2\pi ib} e^{-2\pi i b} \int_1^0 f

\left(1-e^{2\pi i b}\right) \int_0^1 f+e^{2\pi i a} e^{2\pi i b} \int_0^1 f-e^{2\pi i a} \int_0^1

\left(1-e^{2\pi i b}\right)\int_0^1 f-e^{2\pi i a}\int_0^1 f\left(1-e^{2\pi i b}\right)

\left(1-e^{2\pi i a}\right)\left(1-e^{2\pi i b}\right)\int_0^1 f=\int_P fdz

\left(1-e^{2\pi i a}\right)\left(1-e^{2\pi i b}\right)\beta(a,b)=\int_P fdz

This has got to be one of the most beautiful concepts I have ever seen in Complex Analysis!

 

[epr1990]

There are a vast number of beautiful results in complex analysis. This is indeed one of them. May I ask what plotting utility you used?

 

[jackmell]

There are a vast number of beautiful results in complex analysis. This is indeed one of them. May I ask what plotting utility you used?

Mathematica. However I just hand-drew the pochhammer contour with the graphics tools and then used a routine I wrote to Fourier-smooth it. The other contour I also drew by hand with just a combination of circles and lines with hit-and-miss coordinates until I got it looking good.

 

[epr1990]

Awesome, thanks. I haven't used mathematica in a few years. Actually, last time I used mathematica I don't even think I knew what a contour was. I have been using python lately to do everything computationally/graphically. It would be awesome though to not have to literally write my own program to do stuff like this every time though.

 

[jackmell]

I wish to begin a detailed analysis of this problem and welcome comments. I believe the published integral expression for the beta function continuation

$$\left(1-e^{2\pi i\alpha}\right)\left(1-e^{2\pi i\beta}\right)\beta(\alpha,\beta)=\int_P z^{\alpha-1}(1-z)^{\beta-1}dz$$

is misleading in that it is only valid if the correct determination of the integrand is used at the start of integration. However, as I am new to this concept, I could be wrong and if so, I hope someone reading this thread can help me understand it better. This analysis includes what I believe it one of the most difficult concepts in Complex Analysis for new students to master: computing the analytically-continuous argument change of a function around a contour or $\Delta_C \text{arg}(f)$. So I hope those interested in the topic will find the following helpful.

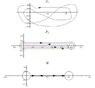
The following three forms of the pochhammer contour are useful. The four horizontal paths along the real axis over the $P_2$ and $W$ contours are over different determinations of the function:

Consider the computation of $\beta(\alpha,\beta)$ with $\alpha=3/2$ and $\beta=4/3$ using the pochhammer integral

$$\int_P z^{1/2} (1-z)^{1/3} dz=\int_P fdz.$$

Now consider the complex function $\sqrt[6]{z^3(1-z)^2}$. This function is a six-valued function and therefore the pochhammer contour can traverse the function in six different ways depending upon which determination of the function the integration begins on. In order to unambigously identify these six determinations, consider the algebraic function, $w(z)$ defined as

$$z^3(1-z)^2-w^6=0$$

Arrange the non-zero singular points, $s_i$, of the function in increasing order of absolute value. Take one-half of the smallest member, $s_1$ and identify the reference point $z_0=1/2 |s_1|$. Compute $f(z_0,w)=0$ and arrange the values in order of increasing real part then increasing imaginary part to obtain the list $(w_1,w_2,\cdots, w_n)$. The determinations of this function can now be unambiguously identified by analytic continuation from these reference points. Now consider

$$I_n=\int_{W_n} f dz$$

where the $n$ reflects the particular determination of $f$ used at the start of integration, $z=1/10$ along the blue contour. The following table summarizes numerical results for all determinations.

$$
\begin{array}{|c|c|}
\hline
n & I_n\\
\hline
1 & -1.37669-0.794831 i \\
2 & 1.37669\, +0.794831 i \\
3 & -2.18\times 10^{-7}-1.58966 i \\
4 & -1.37669+0.794831 i \\
5 & 1.37669\, -0.794831 i \\
6 & 2.18 \times 10^{-7}+1.58966 i \\
\hline
\end{array}
$$
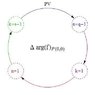
We now go back to the $P_2$ contour and begin the analysis of computing $\Delta \text{arg}$ of the function as we proceed around the contour beginning at the point $z=1/10$ and for that analysis, we write the function as:

$$f=|z|^{1/2}e^{i/2(\theta_p+2n\pi)}|1-z|^{1/3}e^{i/3(\theta_q+2k\pi)}, \quad n=0,1,\quad k=0,1,2$$

with $\theta_p=\text{Arg}(z),\quad \theta_q=\text{Arg}(1-z)$ and $-\pi<\text{Arg}(u)\leq \pi$. In this particular case, we wish to begin the integration of the principle value of the integrand over the blue contour which in the standard order above is the determination identified by $w_2$. As we proceed along the blue contour, the argument does not change. At the point $x=9/10$, we begin around the circular arc with $z=1+\rho e^{it}$ as $t$ varies from $\pi$ to $-\pi$. The argument of the first term does not change, however, the mapping of $(1-(1+\rho e^{it})$ as t goes around this circle is a circle contour around the origin going in a clockwise direction beginning at $\rho$. When $t=0$ we have for the second term $e^{i/3(-\pi)}$ and for the path to be analytically continuous across the negative real axis, we must join the current branch with the branch $e^{i/3(\theta_q+4\pi)}=e^{5\pi i/3}=e^{-\pi i/3}$ and therefore we have $e^{4\pi i/3}f$ for the value of the integrand along the purple contour. Again, the argument does not change along the horizontal leg of the contour. At the point $z=1/10$, we now consider the argument change of $z^{1/2}$. We then have $e^{i/2(\theta_p+2n\pi)}$. As we go around the circular leg in a counterclockwise direction, we reach the point $z=-1/10$ and have $e^{i/2(\pi)}$ and similar to the above, in order to maintain analytic continuity around the contour, we join the current branch with $e^{i/2(\theta_p+2\pi)}=e^{i/2(-\pi+2\pi)}=e^{i/2(\theta_p+2\pi)}$ and proceed to the orange contour at which point we now have $e^{i/2(2\pi)}e^{i/3(4\pi)}f$. We do similar analyses along the entire contour and then consider the limit as the radius, $\rho$ around the two singular points approach zero. We are then left with the horizontal legs and have$$\begin{align*}
\lim_{\rho\to 0}\int_{W_2} fdz&=
\int_0^1 f-e^{4\pi i/3}\int_0^1 f+e^{2\pi i/2}e^{4\pi i/3}\int_0^1 f-e^{2\pi i/2}e^{2\pi i/3}e^{4\pi i/3}\int_0^1 f\\
&=\left(1-e^{4\pi i/3}\right)\int_0^1 f+e^{2\pi i/2}e^{4\pi i/3}\int_0^1 f-e^{2\pi i/2}\int_0^1 f\\
&=\left(1-e^{4\pi i/3}\right)\int_0^1 f+e^{2\pi i/2}\left(e^{4\pi i/3}-1\right) \int_0^1 f\\
&=\left(1-e^{2\pi i/2}\right)\left(1-e^{4\pi i/3}\right)\int_0^1 fdz
\end{align*}
$$

but $e^{4\pi i(1/3)}=e^{4\pi i(4/3-1)}=e^{4\pi i \beta}$ and $e^{2\pi i/2}=e^{2\pi i(3/2-1)}=e^{2\pi i\alpha}$ so that

$$\left(1-e^{2\pi i\alpha}\right)\left(1-e^{4\pi i\beta}\right)\int_0^1 z^{1/2}(1-z)^{1/3}dx=\lim_{\rho\to 0}\int_{W_2} z^{1/2}(1-z)^{1/3}dz$$

or:

$$\left(1-e^{2\pi i\alpha}\right)\left(1-e^{4\pi i\beta}\right)\beta(\alpha,\beta)=\int_{W_2} z^{1/2}(1-z)^{1/3}dz$$

which is consistent with numerical results since:

$$\frac{I_2}{\left(1-e^{2\pi i\alpha}\right)\left(1-e^{4\pi i\beta}\right)}\approx 0.458896 - 7.16\times10^{-9}i\approx \beta(3/2,4/3)$$

Note this is not in the form of the standard integral expression of the beta function continuation.

 

[jackmell]

Before going further with this analysis, I thought it would be helpful to ground the reader in the actual integration path of this problem. The pochhammer contour is unusual in that it is not a simple contour like the common contours studied in basic complex analysis. Just looking at the three diagrams above does not give the reader a sense of what actually is being integrated. The figure below shows explicitly, one of six ways the contour worms through the real component of the function $z^{1/2}(1-z)^{1/3}$, a different determination of the function being traversed over the horizontal blue, green, red and purple legs. In this particular case, the start of integration, blue, is pinned on the principle value of the function; if you just plotted the function $f(x)=x^{1/2}(1-x)^{1/3}$, for $(0.3,0.7)$, the resulting plot would be the same as the blue contour.The figure only shows a small part of the function's total coverings in order to see more clearly how the pochammer contour winds through the various sheets. The full real component of the function for $|z|\leq 2$ , for those interested, is shown in the thumbnail below. If you click on it, you can just barely make out some of the contour embedded deep in the twisted sheets of the function.

 

[jackmell]

We now compute the remaining five integral expressions for this beta continuation. But before we do that, I want to point out an important property of the pochhammer contour resulting for the analysis of $\Delta_P \text{arg}(f)$: the pochhammer path around this function is a closed loop. That is, it returns to its starting point. Keep in mind, just because the contour is closed, does not mean the path is. For example, the closed contour $z=e^{it}$ around the complex log function is obviously not closed as the end point does not return to the start point. How do we know the pochhammer path is closed? Easy: by studying the argument change around the path. Consider the changes computed above:

$$ f\to e^{4\pi i/3}f\to e^{2\pi i/2}e^{4\pi i/3}f\to e^{2\pi i/2}e^{4\pi i/3}e^{2\pi i/3}f$$

and although we did not have to calculate it for the problem, the argument change around the final circuit about the origin was again $e^{2\pi i/2}$. This then gave us:

$$ f\to e^{4\pi i/3}f\to e^{2\pi i/2}e^{4\pi i/3}f\to e^{2\pi i/2}e^{4\pi i/3}e^{2\pi i/3}f\to e^{2\pi i/2}e^{2\pi i/2}e^{4\pi i/3}e^{2\pi i/3}f=f$$

The pochhammer contour returns to the starting branch as could be seen by the illustration showing the contour over the real component of the function and no doubt is the case for all beta continuation expressions although I cannot at present prove this.

Once we have the principal-valued integral expression, we can easily compute the remaining expressions. For example, $w_3$ in the standard order corresponds to the branch $e^{4\pi i/3}f$. Then the integral expression about this particular path is just:

$$e^{4\pi i/3}\left(1-e^{4\pi i/3}\right)\left(1-e^{2\pi i/2}\right)\beta(\alpha,\beta)=\int_{w_3} f dz$$

or:

$$-e^{2\pi i/3}\left(1-e^{2\pi i/3}\right)\left(1-e^{2\pi i/2}\right)\beta(\alpha,\beta)=\int_{w_3} f dz$$

The remaining expressions are likewise computed. The following summarizes all routes:


$$\begin{align}
-2\left(1-e^{4\pi i/3}\right)\beta(\alpha,\beta)&=\int_{w_1} f dz \\
\left(1-e^{4\pi i/3}\right)\left(1-e^{2\pi i/2}\right)\beta(\alpha,\beta)&=\int_{w_2} f dz \\
\displaystyle -e^{2\pi i/3}\left(1-e^{2\pi i/3}\right)\left(1-e^{2\pi i/2}\right)\beta(\alpha,\beta)&=\int_{w_3} f dz\\
\displaystyle \left(1-e^{2\pi i/3}\right)\left(1-e^{2\pi i/2}\right)\beta(\alpha,\beta)&=\int_{w_4} f dz \\
\displaystyle -\left(1-e^{2\pi i/3}\right)\left(1-e^{2\pi i/2}\right)\beta(\alpha,\beta)&=\int_{w_5} f dz\\
\displaystyle e^{2\pi i/3}\left(1-e^{2\pi i/3}\right)\left(1-e^{2\pi i/2}\right)\beta(\alpha,\beta)&=\int_{w_6} f dz\\
\end{align}
$$

and these are again confirmed by numerical calculations. Notice there is only one route that yields the standard integral expression, the $w_4$ route. This raises several questions:

(1) Is it possible to determine which route yields the standard integral expression without first actually computing the various argument changes around the route?

(2) Are there more than one route that leads to the standard expression?

 

[jackmell]

Before I attempt to characterize this analytic extension for all $(\alpha,\beta)\in \mathbb{Q}$, I'd like to work a specific example for which the analytic extension is actually needed since the Euler integral form of the beta function
$$\beta(\alpha,\beta)=\int_0^1 x^{\alpha-1}(1-x)^{\beta-1}dx$$

converges only for $\text{Re}(\alpha,\beta)>0$. So I wish to consider

$$\int_P z^{-3/4}(1-z)^{-7/5}dz=\int_P fdz$$

corresponding to $\beta(1/4,-2/5)$.

Taking the reference point $z=1/2$ along the real axis, I again standardize the branches into the set $\{w_1,w_2,\cdots,w_{20}\}$ and then pin the beginning Pochhammer leg, blue, along the principal branch which in this case is $w_2$. Following the technique above, it is then a simple matter to analyze $\Delta_{W_2} \text{arg}(f)$ and arrive at the argument sequence along this contour as

$$f\to e^{\frac{-6\pi i}{5}}f\to e^{\frac{-3\pi i}{2}}e^{\frac{-6\pi i}{5}}f\to e^{\frac{6\pi i}{5}}e^{\frac{-3\pi i}{2}}e^{\frac{-6\pi i}{2}}f\to e^{\frac{3\pi i}{2}}e^{\frac{6\pi i}{5}}e^{\frac{-3\pi i}{2}}e^{\frac{-6\pi i}{5}}f\to f$$

which then translates into

$$\begin{align}
\int_{W_2} z^{-3/4}(1-z)^{-7/5}dz&=\int_a^b fdz\\
&-e^{\frac{-6\pi i}{5}}\int_a^b fdz\\
&+e^{\frac{-3\pi i}{2}}e^{\frac{-6\pi i}{5}}\int_a^b fdz\\
&-e^{\frac{6\pi i}{5}}e^{\frac{-3\pi i}{2}}e^{\frac{-6\pi i}{5}}\int_a^b fdz\\
&+\sum_{n=1}^4 \int_{\rho_n} fdz
\end{align}
$$

where this time I'm not integrating from zero to one and I'm including paths around the singular points since we can no longer use Euler's form of the integral. This can be written as

$$\left(1-e^{\pi i/2}\right)\left(1-e^{4\pi i/5}\right)\int_a^b fdz+\sum_{n=1}^4 \int_{\rho_n} fdz=\int_{W_2}fdz.$$

However, since $W_2$ is homologous to the limiting contour with $\rho\to 0, a\to 0, b\to 1$, and the integral over this limiting case is equal to Euler's integral for $\text{Re}(\alpha,\beta)>0$, by the Principle of Analytic Continuation, we can write

$$\left(1-e^{\pi i/2}\right)\left(1-e^{4\pi i/5}\right)\beta(1/4,-2/5)=\int_{W_2}fdz$$

which is again consistent with numerical calculations since

$$\frac{\int_{W_2} fdz}{\left(1-e^{\pi i/2}\right)\left(1-e^{4\pi i/5}\right)}\approx 1.81999 +8.82627\times 10^{-14}i\approx \beta(1/4,-2/5).$$

The remaining 19 integral forms are easily computed from this principal form as described above.

 

[jackmell]

I wish to determine for a particular starting branch of the function $w=z^{r/s}(1-z)^{p/q}$, which branches are traverses along the pochhammer route. If we begin on the principal branch at say $z=3/10$ over the blue contour in the figure below, then by analyzing the argument change of the function around blue-dashed route, we arrive at the following expression:

$$e^{p/q i(\pi+2n\pi)}=e^{p/qi(-\pi)}$$
or:
$$e^{2n\pi i p/q}=e^{-2\pi ip/q}$$

Now, with Jacqueline's help in this thread:

https://www.physicsforums.com/showthread.php?t=723675

we have

$$e^{2n\pi i p/q}=e^{-2\pi ip/q+jk\pi i},\quad n=1,2,\cdots,q-1 \quad \text{and }k\in \mathbb{Z}$$

or:

$$2\pi i(np/q)=2\pi i(j-p/q)$$
$$ np=jq-p$$
$$ (n+1)=j(q/p)$$

Since I know beforehand that there can be only one solution to this problem, one n only, I can always let $j=p$ which means the ending branch will always be $q-1$. Likewise, over the purple-dashed contour, we have
$$e^{2\pi ir/s}=e^{2\pi ir/s+2j\pi i}$$
$$kr/s=\frac{r+sj}{s}$$
$$k-1=sj/r$$

and therefore since there can be only one $k$ in the range of $\{1,s-1\}$, choose $j=0$ and therefore, the next branch will always be the $k=1$ branch.

Over the red-dashed contour, we have

$$e^{2n\pi ip/q}=e^{2\pi ip/q+jk\pi i}$$
$$np=p+jq$$
$$n-1=jp/q$$

and so again, we let j=0 so that $n=1$ is the new branch number.

On the final contour:

$$e^{2k\pi ir/s}=e^{-2\pi ir/s+2j\pi i}$$
or:

$$kr+r=sj$$
$$k+1=sj/r$$

we again let j=r so that k=s-1. These argument changes are depicted in the following plot.

It shows that traversing over the blue-dashed contour changes the branch to the $n=q-1$ branch. As we next go around the purple-dashed contour, the branch changes to the $k=1$ branch and so forth around the contour.

For $w=z^{r/s}(1-z)^{p/q}$, we then have over the principle contour:

$$\int_0^1 f+a\int_1^0 f+ab\int_0^1 f+abc \int_1^0 f$$

where $a=e^{2\pi ip/q(q-1)}$, $b=e^{2\pi ir/s}$, and $c=e^{2\pi ip/q}$.

or:

$$(1-a)(1-b)\int_0^1 fdz=\int_{P(0,0)} fdz$$

or:

$$\left(1-e^{2\pi i\alpha}\right)\left(1-e^{-2\pi i\beta}\right)\beta(\alpha,\beta)=\int_{P(0,0)} z^{\alpha-1}(1-z)^{\beta-1}dz$$

where the $P(0,0)$ signifies that we are pinning the starting branch, blue, on the principle branch or k=0 and n=0 branch.

 

[jackmell]

I'd like to finish up my preliminary work with this subject by considering the general case of $(\alpha,\beta)\in\mathbb{C}$.

We can treat both irrational and complex exponents identically as they both involve logarithmic branchings as opposed to algebraic branching in the rational case. For:
$$w=z^a(1-z)^b,\quad (a,b)\in \mathbb{C}$$
we write the function as
$$w=e^{a(\ln|z|+i(\theta_1+2k\pi))}e^{b(\ln|1-z|+i(\theta_2+2n\pi))}$$
and using the same procedure as above, we find the argument change over the contour follows:
$$f\to e^{-2\pi ib}f\to e^{-2\pi ib}e^{2\pi ia}f\to e^{2\pi ib}e^{-2\pi ib}e^{2\pi ia}f\to e^{-2\pi ia}e^{2\pi ib}e^{-2\pi ib}e^{2\pi ia}f.$$
And therefore the argument change follows the sequence $n=-1, k=1, n=1, k=-1$.
The integrals then become
$$\int_P fdz=\int_0^1 fdz-e^{-2\pi i b}\int_0^1 fdz+e^{-2\pi ib}e^{2\pi ia}\int_0^1 fdz-e^{2\pi i a}\int_0^1$$
or
$$\left(1-e^{2\pi i \alpha}\right)\left(1-e^{-2\pi i \beta}\right)\beta(\alpha,\beta)=\int_{P(0,0)} fdz.$$
But we can write the argument change for rational exponents using the same branching changes. That is, the rational case of $n=q-1$ is equivalent to $n=-1$ and likewise for the $k$ branches.


Conclusions:

I do not believe the widely-published expression for the beta function continuation via the pochammer integral:

$$\left(1-e^{2\pi i \alpha}\right)\left(1-e^{2\pi i \beta}\right)\beta(\alpha,\beta)=\int_C t^{\alpha-1}(1-t)^{\beta-1}dt$$

is correct for all $(\alpha,\beta)\in \mathbb{C}$ and is only correct when $(\alpha,\beta)\in \mathbb{Q}$ and a particular set of determinations are selected for the integration path. A more general expression is:

$$e^{2k\pi i\alpha} e^{2n\pi i\beta}\left(1-e^{2\pi i \alpha}\right)\left(1-e^{-2\pi i \beta}\right)\beta(\alpha,\beta)=\mathop\oint\limits_{P(k,n)} z^{\alpha-1}(1-z)^{\beta-1}dz$$

valid for all $(\alpha,\beta)\in \mathbb{C}$ and clearly indicates how the left side of the expression depends upon which function determinations the pochhammer contour traverses.

 

[jackmell]

I do not believe the widely-published expression for the beta function continuation via the pochammer integral:

$$\left(1-e^{2\pi i \alpha}\right)\left(1-e^{2\pi i \beta}\right)\beta(\alpha,\beta)=\int_C t^{\alpha-1}(1-t)^{\beta-1}dt$$

is correct . . .

There is more than one form of the pochhammer contour, the set, a sort of "mirror images" of one another. And the slight differences in them lead to slightly different forms of the beta function continuation expression. I'll leave for the reader then, the discovery of these isomers of the pochhammer contour. In one form, the circuit around the contour goes around one in the negative sense, then zero positive, one positive, then zero negative. This particular route is then reflected in the argument change around the circuit as

$$ f\to e^{-2\pi i b}f\to e^{-2\pi i b}e^{2\pi i a}f\to e^{-2\pi i b}e^{2\pi ib} e^{2\pi ia}f\to e^{-2\pi i a}e^{-2\pi i b}e^{2\pi ib} e^{2\pi ia}f$$

or in a more compact form, (-1,+0,+1,-0). And that leads to

$$\left(1-e^{2\pi i \alpha}\right)\left(1-e^{-2\pi i \beta}\right)\beta(\alpha,\beta)=\oint_P z^{\alpha-1}(1-z)^{\beta-1}dz.$$

However, if we choose the route (-1,-0,+1,+0), we obtain

$$\left(1-e^{2\pi i \alpha}\right)\left(1-e^{2\pi i \beta}\right)\beta(\alpha,\beta)=\oint_P z^{\alpha-1}(1-z)^{\beta-1}dz.$$

Likewise, a third form (+1,-0,-1,+0) leads to the expression:

$$\left(1-e^{-2\pi i \alpha}\right)\left(1-e^{2\pi i \beta}\right)\beta(\alpha,\beta)=\oint_P z^{\alpha-1}(1-z)^{\beta-1}dz$$

with the requirement, in all cases, that integration pins on the principal branch and follows an analytically-continuous route over the function. Perhaps a better form would be

$$\left(1-e^{2\pi i \alpha}\right)\left(1-e^{2\pi i \beta}\right)\beta(\alpha,\beta)=\mathop\oint\limits_{P(-1,-0,+1,+0)} z^{\alpha-1}(1-z)^{\beta-1}dz$$

but that's just too messy. What if we adopt a convention of using the pochhammer isomer which gives rise to positive exponents. In that case I could see writing:

$$\left(1-e^{2\pi i \alpha}\right)\left(1-e^{2\pi i \beta}\right)\beta(\alpha,\beta)=\oint_P z^{\alpha-1}(1-z)^{\beta-1}dz$$

and I like the circle through the integral to emphasize it is true only along an analytically-continuous and closed loop. However, those in the know, unlike me, would already know the pochhammer contour is by design, a closed-loop contour, and what's more, if the problem concerns analytic-continuation, then obviously the integration is an analytically-continuous route over the branch coverings. Then we could dispense with the excess decorating and simply write

$$\left(1-e^{2\pi i a}\right)\left(1-e^{2\pi i b}\right)\beta(a,b)=\int_P z^{a-1}(1-z)^{b-1}dz,\quad (a,b)\in \mathbb{C}.$$