Discussion Overview
The discussion revolves around the relationship between normal modes and degrees of freedom in oscillatory systems. Participants explore whether the number of normal modes is always equal to the number of degrees of freedom, particularly in systems where coordinates can oscillate harmonically. The conversation includes theoretical considerations, mathematical formulations, and specific examples involving a system with four degrees of freedom.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants propose that the number of normal modes is equal to the number of degrees of freedom, but question if this holds for all systems or only those with harmonic oscillation.
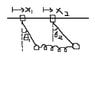
- Others argue that the system described has four normal modes, regardless of mass differences, and that normal modes correspond to oscillations with the same frequency.
- A participant mentions the need for linearization about a stable equilibrium to obtain real frequencies, raising doubts about the applicability of "normal modes" in systems without stable equilibria.
- Concerns are raised about the existence of degenerate frequencies, where multiple normal modes may share the same frequency.
- Discussion includes the mathematical formulation of the characteristic equation for finding normal frequencies and the implications of eigenvalue multiplicity on the number of normal modes.
- Participants explore the potential energy function related to the system and its implications for the symmetry of the stiffness matrix.
Areas of Agreement / Disagreement
Participants express differing views on the conditions under which the number of normal modes equals the number of degrees of freedom. There is no consensus on whether this holds universally or under specific conditions, and the discussion remains unresolved regarding the implications of linearization and the existence of degenerate frequencies.
Contextual Notes
Limitations include the dependence on assumptions about the system's stability and the nature of oscillations. The discussion also highlights unresolved mathematical steps related to the characteristic equation and the potential energy function.
Who May Find This Useful
This discussion may be of interest to those studying oscillatory systems in physics, particularly in the context of normal modes, degrees of freedom, and mathematical modeling of physical systems.