You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is Aharonov-bohm: Definition and 18 Discussions
The Aharonov–Bohm effect, sometimes called the Ehrenberg–Siday–Aharonov–Bohm effect, is a quantum mechanical phenomenon in which an electrically charged particle is affected by an electromagnetic potential (φ, A), despite being confined to a region in which both the magnetic field B and electric field E are zero. The underlying mechanism is the coupling of the electromagnetic potential with the complex phase of a charged particle's wave function, and the Aharonov–Bohm effect is accordingly illustrated by interference experiments.
The most commonly described case, sometimes called the Aharonov–Bohm solenoid effect, takes place when the wave function of a charged particle passing around a long solenoid experiences a phase shift as a result of the enclosed magnetic field, despite the magnetic field being negligible in the region through which the particle passes and the particle's wavefunction being negligible inside the solenoid. This phase shift has been observed experimentally. There are also magnetic Aharonov–Bohm effects on bound energies and scattering cross sections, but these cases have not been experimentally tested. An electric Aharonov–Bohm phenomenon was also predicted, in which a charged particle is affected by regions with different electrical potentials but zero electric field, but this has no experimental confirmation yet. A separate "molecular" Aharonov–Bohm effect was proposed for nuclear motion in multiply connected regions, but this has been argued to be a different kind of geometric phase as it is "neither nonlocal nor topological", depending only on local quantities along the nuclear path.Werner Ehrenberg (1901–1975) and Raymond E. Siday first predicted the effect in 1949. Yakir Aharonov and David Bohm published their analysis in 1959. After publication of the 1959 paper, Bohm was informed of Ehrenberg and Siday's work, which was acknowledged and credited in Bohm and Aharonov's subsequent 1961 paper. The effect was confirmed experimentally, with a very large error, while Bohm was still alive. By the time the error was down to a respectable value, Bohm had died.
View More On Wikipedia.org
The most commonly described case, sometimes called the Aharonov–Bohm solenoid effect, takes place when the wave function of a charged particle passing around a long solenoid experiences a phase shift as a result of the enclosed magnetic field, despite the magnetic field being negligible in the region through which the particle passes and the particle's wavefunction being negligible inside the solenoid. This phase shift has been observed experimentally. There are also magnetic Aharonov–Bohm effects on bound energies and scattering cross sections, but these cases have not been experimentally tested. An electric Aharonov–Bohm phenomenon was also predicted, in which a charged particle is affected by regions with different electrical potentials but zero electric field, but this has no experimental confirmation yet. A separate "molecular" Aharonov–Bohm effect was proposed for nuclear motion in multiply connected regions, but this has been argued to be a different kind of geometric phase as it is "neither nonlocal nor topological", depending only on local quantities along the nuclear path.Werner Ehrenberg (1901–1975) and Raymond E. Siday first predicted the effect in 1949. Yakir Aharonov and David Bohm published their analysis in 1959. After publication of the 1959 paper, Bohm was informed of Ehrenberg and Siday's work, which was acknowledged and credited in Bohm and Aharonov's subsequent 1961 paper. The effect was confirmed experimentally, with a very large error, while Bohm was still alive. By the time the error was down to a respectable value, Bohm had died.
View More On Wikipedia.org
-

A Interpretations of the Aharonov-Bohm effect
It was originally argued by Aharonov and Bohm, and by many others, including me in https://arxiv.org/abs/2205.05986 , that the AB effect is most naturally interpreted as the argument that the gauge potential is "real" ontic entity. On the other hand, many, including @vanhees71 , argue that it...- Demystifier
- Thread
- Replies: 249
- Forum: Quantum Interpretations and Foundations
-
K
I Gauge in the Aharonov Bohm effect
In p.385 of Griffiths QM the vector potential ##\textbf{A} = \frac{\Phi}{2\pi r}\hat{\phi}## is chosen for the region outside a long solenoid. However, couldn't we also have chosen a vector potential that is a multiple of this, namely ##\textbf{A} = \alpha \frac{\Phi}{2\pi r} \hat{\phi}## where...- KDPhysics
- Thread
- Replies: 4
- Forum: Quantum Physics
-

A Aharonov - Bohm effect exercise
Does anyone know the answers to this, or can hopefully guide me to a text that will help me solve this aharonov-bohm problem? Here is the given: Particles (of mass m, and charge q), are driven through two slits that have distance d between them, in a screen that is far away (L>>d) from the...- dude2
- Thread
- Replies: 9
- Forum: Atomic and Condensed Matter
-

A Experimental evidence of non-local quantum forces
Becker et al. 2019, Asymmetry and non-dispersivity in the Aharonov-Bohm effect The paper is open access and published in Nature Communications.- Auto-Didact
- Thread
- Replies: 3
- Forum: Quantum Physics
-
S
I Aharonov-Bohm Effect & Adiabatic Approximation
Hello! I am reading Griffiths book on QM and in the chapter about the adiabatic approximation he introduces the Aharonov-Bohm effect. I am not sure why is this effect an example of adiabatic approximation. The hamiltonian doesn't depend on time as the vector potential is not a function of time...- Silviu
- Thread
-
- Tags
- Aharonov-bohm
- Replies: 1
- Forum: Quantum Interpretations and Foundations
-
V
A Is the Effective Potential the same Quantum Potential?
Is the Effective Potential the same thing we called in QM as "Quantum Potential" ?- vincequantum93
- Thread
- Replies: 1
- Forum: Quantum Physics
-

Ahranov-Bohm Effect for *Electric* Potential Field?
The AB effect has been proved experimentally many times for the case where the EM field is strictly a magnetic flux in a solenoid. But, from what I have read, the AB effect for just an electric potential alone has not been demonstrated yet. Do you believe the AB effect for electric potentials...- LarryS
- Thread
- Replies: 1
- Forum: Quantum Interpretations and Foundations
-
J
Sources to learn about Berry phases and Adiabatic Theorem
Hello, I recently went through Griffiths' Quantum Mechanics text and there is a chapter called the Adiabatic Theorem that includes Berry phase and the Aharonov-Bohm effect. As I found them very interesting, I would appreciate if anyone could provide me with some good sources(books, internet...- Joker93
- Thread
- Replies: 4
- Forum: Quantum Physics
-
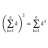
Aharonov-Bohm information propagation
I hope I've searched the forums thoroughly enough, I didn't find a similar question. I'm wondering about the specifics of the speed of the information on change in B of the solenoid between the two paths in a double-slit setup, one large enough where relativistic speed effects are within a...- ddd123
- Thread
- Replies: 2
- Forum: Quantum Interpretations and Foundations
-
B
Aharonov-Bohm Effect: Calculate fringe shift
I am trying to figure out when electrons are subject to an Aharonov-Bohm apparatus (the pick up a phase of +/- e(magnetic_flux)/(h_bar), how the interference fringes are shifted. I know de Broglie wavelength is given by lambda = h/p and that the fringe spacing without the vector potential is...- blankvin
- Thread
-
- Tags
- Aharonov-bohm Fringe Shift
- Replies: 1
- Forum: Quantum Interpretations and Foundations
-

Aharonov-Bohm topological explanation
In trying to get the Aharonov-effect right I've found something that I'm not sure how to sort out. Briefly put my understanding of the effect is that it shows something that cannot be explained by classical physics in the sense that makes observable a classical EM global gauge transformation...- TrickyDicky
- Thread
- Replies: 171
- Forum: Quantum Interpretations and Foundations
-
N
Now what is Aharonov-Bohm really?
I can only seem to find vague sources explaining Aharonov-Bohm, usually saying things as "the different paths of an electron interfere". I presume this is language borrowed from a Feynman path integral formulation of QM, but I'm not familiar with that yet, so I'd rather see it explained in...- nonequilibrium
- Thread
-
- Tags
- Aharonov-bohm
- Replies: 4
- Forum: Quantum Interpretations and Foundations
-
N
Is the Aharonov-Bohm Effect Achievable in Practice?
So the Aharonov-Bohm effect relies on a magnetic field that is only non-zero within a given range. However, is it possible, even in principle (i.e. theoretically), to have such a magnetic field?- nonequilibrium
- Thread
-
- Tags
- Aharonov-bohm
- Replies: 8
- Forum: Quantum Interpretations and Foundations
-
Y
A question on the Aharonov-Bohm effect
We know that Aharonov-Bohm effect is explained by quantum theory. But, I imagine the situation that the solenoid is very far from two-slit. In this case, does Aharonov-Bohm effect happen? Current quantum theory doesn't consider the distance between two-slit and the solenoid. When the...- Younghun park
- Thread
-
- Tags
- Aharonov-bohm
- Replies: 10
- Forum: Quantum Interpretations and Foundations
-
R
Vector Potential applications in Aharonov-Bohm effect
The Aharonov-Bohm effects show how a electro-magnetic field could affect a region of space in which the field had been shielded, although its vector potential did exist there and could interact with the wave function of say the electron. What practical application(s) (so far) can be derived...- riezer
- Thread
- Replies: 3
- Forum: Quantum Interpretations and Foundations
-
G
Help me understand this stuff (re: Aharonov-Bohm Effect, etc.)
Okay, so I was reviewing the Aharonov-Bohm effect online, and found some related discussion on Dirac Monopoles. Let me quote a bit: I don't understand a lick of it. What kind of math do I need to take to understand this stuff? -Geez- Geezer
- Thread
-
- Tags
- Aharonov-bohm
- Replies: 1
- Forum: Advanced Physics Homework Help
-
M
Aharonov-Bohm Effect: Gauge Invariance Consequence
What is the Aharonov-Bohm effect and why it is a conseguence of the gauge invariance?- martyf
- Thread
-
- Tags
- Aharonov-bohm
- Replies: 2
- Forum: Quantum Interpretations and Foundations
-
Aharonov-Bohm Effect: Real or Myth?
Is this thing for real? Have you heard of it? :confused:- Mk
- Thread
-
- Tags
- Aharonov-bohm
- Replies: 2
- Forum: Electromagnetism