1. Complex #'s Proof, 2.Complex Particle movement, Magntitute of Acc. and Vel.

[H2instinct]

Complex Numbers Proof

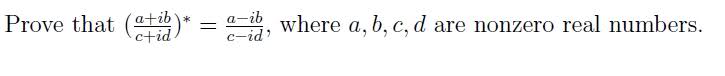
Multiplying the top and bottom by the complex conj. of the bottom:

$$\frac{a+ib}{c+id} * \frac{c-id}{c-id}$$

Gives me:

$$\frac{(ac+bd) - i(ad-bc)}{c^{2}+d^{2}}$$

In form x+iy it is:

$$\frac{(ac+bd)}{c^{2}+d^{2}} + (\frac{(bc-ad)}{c^{2}+d^{2}})*i$$

This is where I get stuck. In order to prove $$\left(\frac{a+ib}{c+id}\right)$$*$$\equiv\frac{a-ib}{c-id}$$ I think that I am supposed to take the complex conjugate of my previous answer and then work backwards until I get to $$\frac{a-ib}{c-id}$$. I have tried this with several different variations and I am not coming up with the proof at all. I need a bump in the right direction here.

 

[lanedance]

i think you're heading right direction, first combine everything on the same denominator, then use the fact
$$c^2+d^2 = (c+id)(c-id)$$

and previously you multiplied
$$(a+ib)(c-id) = (ac+bd) + i(bc-ad)$$

so now use the fact
$$(a+ib)(c+id) = (ac+bd) - i(bc-ad)$$
(check if you need)