10^80 particles in observable v unobservable universe

[robertjford80]

Here is a chart showing the unobservable universe

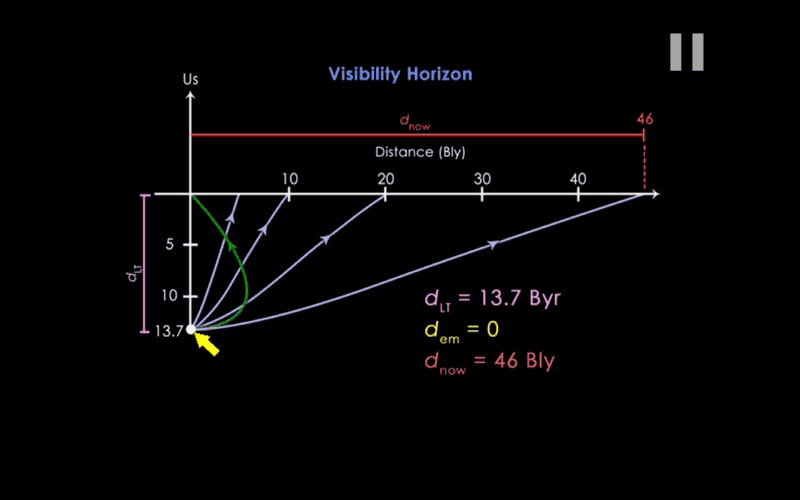
The green lines indicates the part we can see. My question is that figure that gets thrown around, there are 10^80 particles in the universe, is that for observable or the unobservable universe.

 

[nicksauce]

10^80 is for the observable universe, as the unobservable universe is probably [maybe?] infinite.

 

[robertjford80]

that the unobservable universe is not infinite is something i feel very strongly about. it's quite simple: the universe began at a definite time in the past and it is bounded by the present, so there is a boundary on the past and the present, hence finite. Second argument: in an infinite universe there is an infinite amount of matter which would overwhelm the cosmological constant thus causing the universe to implode into a big crunch. third, you can't do any measurements in an infinite universe because all quantities are infinite, thus there is no way to determine if space is flat. fourth, although this is an argument from authority, take a look at the graph, it clearly shows the unobservable universe to be not infinite but finite at roughly 46 billion light years. fifth, you can't calculate probabilities in an infinite universe, the odds of all events happening are infinite. sixth, as olbert demonstrated in the 1830's in an infinite universe the sky would be filled with light from every angle.

 

[nicksauce]

the universe began at a definite time in the past and it is bounded by the present, so there is a boundary on the past and the present, hence finite.

A timelike boundary does not imply a spacelike boundary.

Second argument: in an infinite universe there is an infinite amount of matter which would overwhelm the cosmological constant thus causing the universe to implode into a big crunch.

Plainly false. The Friedmann equations show that the big crunch only results in universes with positive curvature (i.e., finite universes)

third, you can't do any measurements in an infinite universe because all quantities are infinite, thus there is no way to determine if space is flat.

Just do your measurement in some local patch. Why does the rest of the universe matter?

fourth, although this is an argument from authority, take a look at the graph, it clearly shows the unobservable universe to be not infinite but finite at roughly 46 billion light years.

You are way off-base here. 46 Glyr is the size of the **observable** universe.

fifth, you can't calculate probabilities in an infinite universe, the odds of all events happening are infinite.

I don't think this makes any sense.

sixth, as olbert demonstrated in the 1830's in an infinite universe the sky would be filled with light from every angle.

This is true for an infinitely old universe, but is solved by a finite age universe. If the universe is of finite age, there we can only have received light from so far away, so the sky will not be filled with light from every angle, regardless of whether or not the whole universe is infinite.

 

[robertjford80]

A timelike boundary does not imply a spacelike boundary.

Sure it does. Go back to first year physics. Take the following equation:

D = RT, distance equals rate times time. You're arguing the D is infinite. How do you get D to be infinite? Either R or T has to be infinite. What's the R of the universe? It's the Hubble constant, 75 km/s/MPc. What's the T of the universe. It's 13.75 by. Hence D is finite.

Just do your measurement in some local patch. Why does the rest of the universe matter?

That's ridiculous. I have a feeling that you're talking about the multiverse for which there is no evidence. It's the universe as a whole that matters. Let's say my local patch was the solar system and someone else's local patch was the system of Alpha Centauri, clearly our measurements would be in disagreement.

You are way off-base here. 46 Glyr is the size of the **observable** universe.

Look at the chart again. It's that curved green line that represents the observable universe.

I don't think this makes any sense.

What is the probability that I'm a random word generator? How do you determine the probability of something? You take the number of events divided by the probability space. in an infinite universe there is an infinite number of random word generators, moreover, the space in which it can happen is infinite, so you can't determine the probability of something happening.

 

[DaveC426913]

What is the probability that I'm a random word generator? How do you determine the probability of something? You take the number of events divided by the probability space. in an infinite universe there is an infinite number of random word generators, moreover, the space in which it can happen is infinite, so you can't determine the probability of something happening.

Yes you can.

While it is probably true that, in an infinite universe, all things that can happen will happen, so what? our cause and effect is still limited to our own light cone.

Show me one example where something that happens 10³⁰ light years away has any effect on our calculations or physical universe here.

 

[phinds]

that the unobservable universe is not infinite is something i feel very strongly about.

Yes, but the universe really doesn't care what you think, and as nicksauce has pointed out, your logic is seriously flawed.

Your inability, or unwillingness, to accept that the universe might have STARTED OUT infinite (weird as that does seem), is your limitation, not the universe's. Just because it was a lot smaller 14+ billion years ago does NOT imply that it was finite.

 

[robertjford80]

Yes you can.

While it is probably true that, in an infinite universe, all things that can happen will happen, so what? our cause and effect is still limited to our own light cone.

Show me one example where something that happens 10³⁰ light years away has any effect on our calculations or physical universe here.

Probability at least can be debated. The following however cannot:

Take the following equation:

D = RT, distance equals rate times time. You're arguing the D is infinite. How do you get D to be infinite? Either R or T has to be infinite. What's the R of the universe? It's the Hubble constant, 75 km/s/MPc. What's the T of the universe. It's 13.75 by. Hence D is finite.

I would like an answer to the above.

 

[robertjford80]

Yes, but the universe really doesn't care what you think, and as nicksauce has pointed out, your logic is seriously flawed.

I'm not saying: I feel strongly about X therefore X is true. I'm saying that X is true, I think it's important. A lot of people think it's false, and I care deeply about this misconception.

For you as well, phinds, I would like an answer to this:

D = RT, distance equals rate times time. You're arguing the D is infinite. How do you get D to be infinite? Either R or T has to be infinite. What's the R of the universe? It's the Hubble constant, 75 km/s/MPc. What's the T of the universe. It's 13.75 by. Hence D is finite.

Your inability, or unwillingness, to accept that the universe might have STARTED OUT infinite (weird as that does seem), is your limitation, not the universe's. Just because it was a lot smaller 14+ billion years ago does NOT imply that it was finite.

This is just a bald assertion. You've got no reason for this statement of faith.

 

[DaveC426913]

You're arguing the D is infinite.

I'm not. I'm simply poking holes in the flawed logic that's been presented.

 

[DaveC426913]

This is just a bald assertion. You've got no reason for this statement of faith.

As is yours. "It is finite" is a statement of faith. You can't apply things like D=R/T to the universe.

More correctly, we think it's probably finite.

 

[Number Nine]

You take the number of events divided by the probability space. in an infinite universe there is an infinite number of random word generators, moreover, the space in which it can happen is infinite, so you can't determine the probability of something happening.

This betrays an ignorance of basic probability. You can certainly calculate probabilities that way when dealing with a finite sample space, but calculus allows us to deal with infinite (or uncountable) probability spaces very easily. The normal distribution itself is, of course, defined over the reals...

Sure it does. Go back to first year physics. Take the following equation:

D = RT, distance equals rate times time. You're arguing the D is infinite. How do you get D to be infinite? Either R or T has to be infinite. What's the R of the universe? It's the Hubble constant, 75 km/s/MPc. What's the T of the universe. It's 13.75 by. Hence D is finite.

You're assuming here that the universe began with radius zero and that expansion involves the increase in radius over time, but this isn't true. Expansion, in the context of the bang bang, refers to metric expansion, which is very different.

 

[Dickfore]

Sure it does. Go back to first year physics. Take the following equation:

D = RT, distance equals rate times time. You're arguing the D is infinite. How do you get D to be infinite? Either R or T has to be infinite. What's the R of the universe? It's the Hubble constant, 75 km/s/MPc. What's the T of the universe. It's 13.75 by. Hence D is finite.

Your equation is dimensionally incorrect.

 

[robertjford80]

You're assuming here that the universe began with radius zero and that expansion involves the increase in radius over time, but this isn't true. Expansion, in the context of the bang bang, refers to metric expansion, which is very different.

You're going to have to show how metric expansion implies an infinite space.

Also an infinite universe conflicts with standard inflationary cosmology. Here's a quote from Lisa Randall

The universe doubled in size in a fixed time and then doubled again in that same time and then kept doubling at least 90 times in a row until the inflationary epoch ended and the universe was as smooth as we see it today. This exponential expansion means, for example, that when the universe’s age had multiplied by 60 times, the size of the universe would have increased by more than a trillion trillion trillions in size.

You can't double the size of the universe if it is infinite.

I also want to get back to the density parameter. You can't calculate the density of an infinite universe. Such statements as the universe is 4% ordinary matter, and 24% dark matter are meaningless because in an infinite universe there is an infinite amount of matter.

 

[robertjford80]

As is yours. "It is finite" is a statement of faith. You can't apply things like D=R/T to the universe.

You're just asserting that you can't apply things like D = RT to the universe. You're going to have to provide some reason why our common sense intuitions should be suspended. If you look at the chart above, it clearly asserts that the size of the universe is 46 billion light years. It doesn't require faith to believe that a finite number times a finite number equals a finite number.

More correctly, we think it's probably finite.

If it's more probable that the universe is finite then we're in agreement. Of course there's always a small probability that the universe is infinite but that's not what we're arguing and that's not what nicksauce asserted.

 

[Number Nine]

You're going to have to show how metric expansion implies an infinite space.

No, you're completely missing the point here. Your argument was as follows: the expansion of the Universe involved the Universe beginning with finite size and increasing in radius over time, therefore the current size of the Universe must be finite. You grossly misunderstand the notion of inflation in Big Bang cosmology; and your argument fails utterly when expansion is understood as metric expansion.

I also want to get back to density parameter. You can't calculate the density of an infinite universe. Such statements as the universe is 4% ordinary matter, and 24% dark matter are meaningless because in an infinite universe there is an infinite amount of matter.

Brilliant! It's incredible that a century's worth of physicists and mathematicians have simply overlooked this fact. If only we had a mathematical framework that allowed us to deal with infinite processes; it's a shame that Isaac Newton didn't think of one...

If you look at the chart above, it clearly asserts that the size of the universe is 46 billion light years.

No, it doesn't. That chart very obviously describes the radius of the observable universe as 46 light-years. It even has a nice caption saying "visibility horizon" above the bar reading 46 light-years. How have you failed to notice this?

 

[Dickfore]

Hey OP, imagine a (infinite) plane. Next, imagine the plane stretching evenly. If you drew two points on it, they would recede from each other. So would any two arbitrary points. Did the size of the plane increase? Next, imagine two distant points and a light signal emanating from the first one towards the second one. If the points are sufficiently far apart, the distance between them would increase by more than the distance traverseed by the light. In this fashion, we arrive at an observable region around each point. Does this region increase?

 

[robertjford80]

You grossly misunderstand the notion of inflation in Big Bang cosmology; and your argument fails utterly when expansion is understood as metric expansion.

You still haven't explained how metric expansion implies an infinite space.

Brilliant! It's incredible that a century's worth of physicists and mathematicians have simply overlooked this fact. If only we had a mathematical framework that allowed us to deal with infinite processes; it's a shame that Isaac Newton didn't think of one...

This is just an assertion. Why don't you demonstrate how you can calculate that the universe is made of 4% ordinary matter when in an infinite universe it should be infinite.

No, it doesn't. That chart very obviously describes the radius of the observable universe as 46 light-years. It even has a nice caption saying "visibility horizon" above the bar reading 46 light-years. How have you failed to notice this?

It's the green line that marks the observable universe. You can't observe something 46 billion light years away because only 13.7 billion years have passed. How have you failed to notice this?

 

[robertjford80]

Hey OP, imagine a (infinite) plane. Next, imagine the plane stretching evenly. If you drew two points on it, they would recede from each other. So would any two arbitrary points. Did the size of the plane increase? Next, imagine two distant points and a light signal emanating from the first one towards the second one. If the points are sufficiently far apart, the distance between them would increase by more than the distance traverseed by the light. In this fashion, we arrive at an observable region around each point. Does this region increase?

Above are self-consistent statements but you have not shown that those statements describe reality. Nor have you shown how they do not conflict with standard inflationary cosmology:

The universe doubled in size in a fixed time and then doubled again in that same time and then kept doubling at least 90 times in a row until the inflationary epoch ended and the universe was as smooth as we see it today. This exponential expansion means, for example, that when the universe’s age had multiplied by 60 times, the size of the universe would have increased by more than a trillion trillion trillions in size.

Further, you have yet to explain how a finite number times a finite number equals an infinite number.

 

[Number Nine]

You still haven't explained how metric expansion implies an infinite space.

I'm tempted to dismiss this as deliberate ignorance. As I've already clearly explained to you, the notion of metric expansion was brought up because you misunderstand what expansion means in the context of big bang cosmology. You argued that the universe must be finite because its radius has expanded at a finite rate since its origin. Your argument is flawed because your premise is wrong; expansion has nothing to do with an increase in the radius of the universe.

This is just an assertion. Why don't you demonstrate how you can calculate that the universe is made of 4% ordinary matter when in an infinite universe it should be infinite.

How can you say that 50% of positive integers are even if there are infinitely many positive integers? You would need some sort of magic!

Infinitude doesn't negate the existence of ratios or probability; I can't imagine why you think it would. There are infinitely many natural numbers and infinitely many primes, but we can still calculate the probability that a randomly selected number less than n is prime (even taking the case where n goes to infinity), and that probability is finite (or do you dismiss complex analysis as well?)

Honestly, have you ever even encountered a normal distribution? We do probability over infinite sample spaces all the time. It's trivial. You would be aware of this if you had even the slightest knowledge of elementary mathematics.

Further, you have yet to explain how a finite number times a finite number equals an infinite number

Why would he? It's irrelevant to the discussion.

 

[robertjford80]

Number nine,

So do you concede that the chart states the unobservable universe is 46 bly across?

I'm tempted to dismiss this as deliberate stupidity. As I've already clearly explained to you, the notion of metric expansion was brought up because you misunderstand what expansion means in the context of big bang cosmology. You argued that the universe must be finite because its radius has expanded at a finite rate since its origin. Your argument is flawed because your premise is wrong; expansion has nothing to do with an increase in the radius of the universe.

You're just asserting that the premise is wrong. You don't have any reasons for why the universe is infinite. You also have yet to comment on the Lisa Randall quote which states that the size of the universe doubled.

What determines the size of the universe other than the Hubble constant and its age? Both of those numbers are finite.

What is "infinite percent" supposed to mean, exactly?

You tell me. You're the one that is asserting that the amount of ordinary matter is 4% in an infinite universe.

Infinitude doesn't negate the existence of ratios or probability; I can't imagine why you think it would. There are infinitely many natural numbers and infinitely many primes, but we can still calculate the probability that a randomly selected number less than n is prime (even taking the case where n goes to infinity), and that probability is finite (or do you dismiss complex analysis as well?)

Less than n is not infinite. Sure, we can calculate the probability of primes less than n but not more than n.

You have a flawed analogy. The ratio of primes to non primes is not analogous to determining the density of an infinite space. To determine the density of space you need to know how large the space is. You can't determine how large infinity is.

Moreover, you can calculate the odds of a number being prime

If this is true, then what are they? You can't tell because you're just guessing that the odds of a prime below 9 digits is more or less similar to the odds of a prime above 9 digits. In order for the density of the universe to be calculated it has to be in principle calculable if not calculable practically. You can't get an exact number with infinity. Infinity divided by infinity equals infinity.

We do probability over infinite sample spaces all the time.

Give me an example.

Further, you have yet to explain how a finite number times a finite number equals an infinite number

Why would he? It's irrelevant to the discussion.

You're just asserting that it's irrelevant. If the size of the universe is not determined by the Hubble parameter and its age, then what determines it.

 

[nicksauce]

Look it's irrelevant what the chart says, or what you think it says. I know 46 Glyr is the radius of the observable universe because it's a simple calculation I've done many times before.

Start with the FRW metric for a flat universe

$$ds^2 = -c^2dt^2 + a^2(t)\left(dr^2 + r^2d\Omega^2\right)$$

The maximum distance (and hence the spatial boundary of the observable universe) will be represented by radially traveling photons, so choose ds^2=0, and d\Omega=0, and you get

$$dr = c\frac{dt}{a(t)}$$

$$R = c\int\frac{dt}{a(t)}$$

$$R = c\int\frac{da}{\dot{a}(t)a(t)}$$

Then use the Friedmann equation

$$\left(\frac{\dot{a}}{a}\right)^2=H_0^2\left(\Omega_Ma^{-3}+\Omega_{\Lambda}\right)$$

to replace $\dot{a}$ and you get

$$R = \frac{c}{H_0}\int_0^1\frac{da}{a^2\sqrt{\Omega_Ma^{-3}+\Omega_{\Lambda}}}$$

Choose H_0 = 72km/s/Mpc, $\Omega_M=0.28$, $\Omega_{\Lambda}=0.72$. Put into Wolfram alpha http://www.wolframalpha.com/input/?...rom+0+to+1+of+(1+/+(x^2*sqrt(0.28x^-3+0.72))) and you get the 46 billion light years.

 

[Number Nine]

So do you concede that the chart states the unobservable universe is 46 bly across?

No. As is explained above, that number refers to the observable universe.

You're just asserting that the premise is wrong. You don't have any reasons for why the universe is infinite. You also have yet to comment on the Lisa Randall quote which states that the size of the universe doubled.

The premise is wrong because your definition of "expansion" is incorrect; this has been clearly explained to you already. Research metric expansion.

You tell me. You're the one that is asserting that the amount of ordinary matter is 4% in an infinite universe.

Yes, so what? Odd numbers constitute 50% of the integers. The fact that there are an infinite number of integers is irrelevant.

Less than n is not infinite. Sure, we can calculate the probability of primes less than n but not more than n.

As I already very clearly explained, we can easily take the limiting case as n goes to infinity. Any introductory treatment of the prime number theorem will explain this to you.

We do probability over infinite sample spaces all the time.

Give me an example.

I'm going to go right ahead and accuse you of being deliberately ignorant, here. Why? Because right in my previous post I gave you the example of the normal distribution, whose domain is the reals. You've really never encountered basic probability theory before, have you?

 

[IsometricPion]

So do you concede that the chart states the unobservable universe is 46 bly across?

The universe as we know it was to hot and dense until ~300,000 years after the big bang for light to propagate through it freely. Therefore, the light that has taken the longest time to reach us was emitted at that time, it is the cosmic microwave background (CMB). The density of matter in the universe is approximately constant everywhere we know of on scales larger than ~300 Million light-years. General relativity (GR) predicts that the universe will either expand forever or eventually contract back to a singularity, depending on the average density of mass-energy (and the nature of dark energy). Only if the average mass-energy was enough to make the universe contract would GR predict that the universe is finite (at least in the simplest possible geometries ref. Wikipedia- Shape of the Universe).

The 46 billion light-years that the image refers to is the co-moving distance to the CMB (Wikipedia- Distance measures (cosmology)). This is the distance that the matter emitting the CMB would be from us if the universe's expansion were frozen today and measured (though by today it would have formed galaxies and such). The green line presumably indicates the path that light we see as the CMB took to reach us. The light from any object we observe today followed the "same" green path (starting at a point closer to the present of course). So, where the blue line that ends up at 10 billion light-years crosses the green line indicates the co-moving distance from us (looks like about 6 billion light-years) at the time light we see today left objects which today are at a co-moving distance of 10 billion light-years (i.e., roughly 7.5 billion years ago). When the light we see today as the CMB was emitted the matter emitting it was at a co-moving distance of about 42 million light-years. This seems to be the sort of information the posted chart conveys.

The green lines indicates the part we can see. My question is that figure that gets thrown around, there are 10^80 particles in the universe, is that for observable or the unobservable universe.

Any figure for the number of particles in the universe is an extrapolation from the known density and properties of matter to large scales (which seems to be valid on the largest scales). For a universe that is approximately flat on large scales the total mass-energy density must be about 9.7x10^-27 kg/m³ (Wikipedia- Friedmann equations) if 4% of that density is ordinary matter then that part would have an average density of about 3.9x10^-28 kg/m³. Most of this mass density would be in the form of protons and neutrons for a number density of about 0.23 m^-3. 46 billion light-years is about 4.4x10²⁶ m, so the co-moving volume today of the part of universe we can see is about 3.5x10⁸⁰ m³. This yields about 8.1x10⁷⁹ particles. Since most of the universe is made of hydrogen and helium there are a similar number of electrons to yield a total of about 1.7x10⁸⁰ particles.

So, it would appear that 10^80 is a reasonable estimate for the number of particles (of ordinary everyday matter) in the part of the universe we have seen via light. It approximately corresponds to the number of particles at any given time between the line labeled "Us" and the blue line that ends at 46 billion light-years.

Note that anything that is a density in the above calculations is a local (or intrinsic) quantity and is well-defined no matter how big the rest of the universe is. At present there is no way to know how big the part of the universe we can't see is; there may not be much of it we cannot see, we might only be able to see a tiny fraction of the universe, or it could be infinite. Wikipedia- Observable universe describes everything I have said and more.

 

[robertjford80]

This is lifted from the wiki article that isometricpion references who was rather kind and polite about the whole thing, I cannot say the same thing for you, number nine:

No evidence exists to suggest that the boundary of the observable universe constitutes a boundary on the universe as a whole, nor do any of the mainstream cosmological models propose that the universe has any physical boundary in the first place, though some models propose it could be finite but unbounded, like a higher-dimensional analogue of the 2D surface of a sphere which is finite in area but has no edge

This website puts the size of the whole universe at 93 billion light years
http://scaleofuniverse.com/

I'm aware that many mainstream physicists believe the size of the whole universe is infinite. For instance here's Stephen Hawking:

in the third kind of Friedmann model, with just the critical rate of expansion, space is flat (and therefore is also infinite

I have not yet heard any decent reason why anyone would think it is infinite and when I say infinite I mean that there is no limit on how many particles, planets or stars it has. If you're talking about a different kind of infinity that you're committing the fallacy of equivocation.

I'm not sure there any point in debating with you, number nine. You use insulting language such as:

I'm tempted to dismiss this as deliberate stupidity. ... I'm going to go right ahead and accuse you of being deliberately ignorant, here.

When you're opponent starts to use language like that he's doing it to cover up the weakness of his position.

You also fail to answer my points. I can't debate with someone who will not answer the questions I put to him. I asked you to prove how metric expansion implies that space is infinite and you failed to do that. There is nothing in metric expansion that makes space infinite. This is lifted from the wiki article on metric expansion:

The metric expansion of space is the increase of distance with time between distant parts of the universe. It is an intrinsic expansion—that is, it is defined by the relative separation of parts of the universe and not by motion "outward" into preexisting space. The universe is not expanding "into" anything outside of itself. A frequently used 2-D analogy is the expansion of the surface of an expanding rubber balloon.

D= RT still applies you just have to calculate rate differently, that is you have to factor in how much space expands while you're crossing over it. The product of two finite numbers is still finite.


I've also asked you three times for an explanation of this quote:

The universe doubled in size in a fixed time and then doubled again in that same time and then kept doubling at least 90 times in a row until the inflationary epoch ended and the universe was as smooth as we see it today. This exponential expansion means, for example, that when the universe’s age had multiplied by 60 times, the size of the universe would have increased by more than a trillion trillion trillions in size.

It's been my experience that when they refuse to answer a point the first time they rarely answer it when you ask them again.

I asked you to go ahead and calculate the probability of a number being prime and you didn't but said that someone else has done it.

Odd numbers constitute 50% of the integers. The fact that there are an infinite number of integers is irrelevant.

Odd numbers are abstract objects they are true by definition. You can't compare abstract objects with concrete objects. There are 50% odd numbers by definition. You can't say:

"I can calculate the odds of an abstract entity, therefore I can calculate the odds of an empirical entity."

Odd numbers are in no way comparable to concrete, ordinary matter. The ratio of a finite patch of space to infinite space is practically zero. Your sample size of the what you can observe compared to what you think exists is next to nothing. It would be ludicrous to extrapolate from an extremely tiny sample to the whole infinite universe if there is an infinite universe.

Because right in my previous post I gave you the example of the normal distribution, whose domain is the reals.

I'm talking about an example in the real world not an example from the abstract world of mathematics that doesn't exist. Go ahead and tell me the probability of finding a certain type of matter in a universe of infinite size and I'm not talking about the matter restricted to our light cone. I want you to calculate the density of matter in an infinite universe.

 

[nicksauce]

This website puts the size of the whole universe at 93 billion light years
http://scaleofuniverse.com/

Why do you think a non-academic website with no citations should carry any weight?

 

[Number Nine]

You also fail to answer my points. I can't debate with someone who will not answer the questions I put to him. I asked you to prove how metric expansion implies that space is infinite and you failed to do that.

This is why I "used language like that". Nowhere did I say that metric expansion implies that "space is infinite". Nowhere. I have already explained to you (three times) the reason for mentioning metric expansion. Read carefully.

I've also asked you three times for an explanation of this quote:

I have already answered you. Again, see "metric expansion".

D= RT still applies

No, it doesn't. As you have been repeatedly told, your argument assumes (incorrectly) that space began with a finite radius and that expansion involves an increase in the radius of the universe. Since this is nonsense, your little equation is irrelevant.

Your sample size of the what you can observe compared to what you think exists is next to nothing. It would be ludicrous to extrapolate from an extremely tiny sample to the whole infinite universe if there is an infinite universe.

Ridiculous. The universe, by almost every shred of existing evidence, is homogeneous and isotropic. We can deduce a great deal of its properties by examining a small patch, just like I can reliably estimate the mean of a normal distribution given a finite sample.

Odd numbers are abstract objects they are true by definition. You can't compare abstract objects with concrete objects. There are 50% odd numbers by definition.

Stop moving the goalpost. Your argument was that we cannot calculate odds or probabilities when dealing with infinities (which is clearly ridiculous, as I just demonstrated); now you've changed your argument into some sort of philosophical opposition to mathematical objects.

 

[thorium1010]

This website puts the size of the whole universe at 93 billion light years
http://scaleofuniverse.com/

Maybe you should try this one where as other have said, that the size of the observable universe is 90 odd billion light years.

http://www.htwins.net/scale2/

 

[robertjford80]

This is why I "used language like that". Nowhere did I say that metric expansion implies that "space is infinite". Nowhere. I have already explained to you (three times) the reason for mentioning metric expansion. Read carefully.

This is what you originally wrote:

You're assuming here that the universe began with radius zero and that expansion involves the increase in radius over time, but this isn't true. Expansion, in the context of the bang bang, refers to metric expansion, which is very different.

So now you're telling me that what you really meant is: space is finite but your conception of the expansion of space is wrong? Why did you even mention metric expansion if it doesn't prove that space is infinite? What reasons do you even have for believing that space is infinite? Now, since you've admitted that metric expansion does not imply that space is infinite you don't even have any reasons for believing in the infinity of space.

No, it doesn't. As you have been repeatedly told, your argument assumes (incorrectly) that space began with a finite radius and that expansion involves an increase in the radius of the universe. Since this is nonsense, your little equation is irrelevant.

That's not what I'm saying. I'm saying that metric expansion does not imply an infinite universe which you've conceded is true.

Ridiculous. The universe, by almost every shred of existing evidence, is homogeneous and isotropic. We can deduce a great deal of its properties by examining a small patch, just like I can reliably estimate the mean of a normal distribution given a finite sample.

What's ridiculous is you dividing a finite number by an infinite number and concluding that the finite section must be exactly like the infinite section. If that is not an unjustified extrapolation then I don't know what is. Newton used that logic when he wrote his three laws of motion and we now know that it failed him.

Stop moving the goalpost. Your argument was that we cannot calculate odds or probabilities when dealing with infinities (which is clearly ridiculous, as I just demonstrated); now you've changed your argument into some sort of philosophical opposition to mathematical objects.

It's not moving the goal post. You can't compare abstract objects to concrete matter. Abstract objects have their properties out of necessity. The properties of matter can change at any time for no reason. Tomorrow all of the laws of physics could change. Matter is under no obligation to remain constant and unchanging, abstract objects are. You can't compare the two.

You again failed to come up with a calculation for the probability of prime numbers. You again failed to explain why standard inflationary cosmology believes the universe doubled in size 90 times or so every 10^-34 seconds, that is to say, it is finite yet you believe it is infinite.

I'm done debating with you. I have enough evidence to conclude that you'll never come up with a reason for why you believe the universe is infinite other than a bunch of insults.

 

[robertjford80]

Why do you think a non-academic website with no citations should carry any weight?

Correct me if I'm wrong but from the orders of magnitude -33 up to 25 it is right, so why should the 26th be any different. In any case 10^26 meters is a lot different than infinity. You haven't put forth any reason either for why you think the universe's size is infinity. All you've done is calculate the Friedman equation to show that the observable universe is 46 bly across.

 

[nicksauce]

Correct me if I'm wrong but from the orders of magnitude -33 up to 25 it is right, so why should the 26th be any different. In any case 10^26 meters is a lot different than infinity. You haven't put forth any reason either for why you think the universe's size is infinity. All you've done is calculate the Friedman equation to show that the observable universe is 46 bly across.

The point was to correct your misconception that the total universe was 46 Glyr in radius, when in reality it is the observable universe that is 46 Glyr. I proved this that this is the case. Apparently now you are moving on to the misconception that the total universe is 93 Glyr across. Again, this is just 2x the number which is the radius of the observable universe.

 

[Dickfore]

Hey OP, would you agree that the Universe is infinite if it is flat?

 

[robertjford80]

Hey OP, would you agree that the Universe is infinite if it is flat?

I realize Hawking believes that but it doesn't make sense. It's a straight-up contradiction. If you believe the universe doubled in size every 10^-34 seconds 90 times then you can't believe the universe is infinite. Moreover, if the expansion rate is finite, even if it is metric, and the age of the universe is finite, then the size of the universe is finite.

 

[robertjford80]

The point was to correct your misconception that the total universe was 46 Glyr in radius, when in reality it is the observable universe that is 46 Glyr. I proved this that this is the case.
Apparently now you are moving on to the misconception that the total universe is 93 Glyr across. Again, this is just 2x the number which is the radius of the observable universe.

Yes I understand that now. But I do not accept the claim that the universe is probably infinite. Here's a quote from wiki

A 2004 paper by Cornish et al claims to establish a lower bound of 24 gigaparsecs (78 billion light-years) on the diameter of the whole universe, meaning the smallest possible diameter for the whole universe would be only slightly smaller than the observable universe (since this is only a lower bound, the paper leaves open the possibility that the whole universe is much larger, even infinite)

As I've already stated roughly five times I see no reason why anyone would think the universe is infinite when they believe that it was finite at 10^-34 seconds.

 

[Number Nine]

I realize Hawking believes that but it doesn't make sense. It's a straight-up contradiction. If you believe the universe doubled in size every 10^-34 seconds 90 times then you can't believe the universe is infinite. Moreover, if the expansion rate is finite, even if it is metric, and the age of the universe is finite, then the size of the universe is finite.

This has been very clearly explained to you several times, by several different people. The fact that you are still repeating this nonsense about the Universe growing in size suggests that you either aren't interested in learning anything about cosmology, or that you just aren't ready to been taking an interest in physics, because you clearly aren't understanding the very basic explanations that people are putting forward. Personally, I think you're just a crank. The reason you're a crank is that you seem to genuinely believe that you have discovered some sort of trivial logical argument (finite times finite equals finite!11!) that every physicist and mathematician in the world has simply overlooked, and that, by this argument, you have undermined all of the work that has been done in cosmology over the last hundred years. This honestly reminds of the classic creationist talking point whereby every scientist in the world has simply failed to notice that evolution violates the laws of thermodynamics.

Metric expansion refers to the fact that, on a large scale, the distances between objects in the cosmos is increasing. It does not, and I repeat this for the fifth time, it does not mean that the radius of the Universe is is increasing, or expanding out into something. You should consider the possibility that the entirely of the scientific community, which seems to have no problem with the notion of an infinite Universe, may know a tad bit more than you do.

As I've already stated roughly five times I see no reason why anyone would think the universe is infinite when they believe that it was finite at 10^-34 seconds.

Where has anyone argued that the Universe began with finite radius and has since become infinite? The authors establish a lower bound for the diameter of the universe at 10^-34 seconds; so what? What does that have to do with your argument?