karush
Gold Member
MHB
- 3,240
- 5
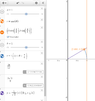
$\textsf{a. Sketch the region of integration and evaluate.}\\$
\begin{align*}\displaystyle
\int_{6}^{\frac{\pi}{6}}
\int_{0}^{\sec{\theta}}
6r^{3} drd\theta\\
W|A=\frac{5}{3\sqrt{3}}
\end{align*}
OK I really didn't know how to do this in desmos
\begin{align*}\displaystyle
\int_{6}^{\frac{\pi}{6}}
\int_{0}^{\sec{\theta}}
6r^{3} drd\theta\\
W|A=\frac{5}{3\sqrt{3}}
\end{align*}
OK I really didn't know how to do this in desmos