18 Free body diagrams, statics

[jonjacson]

Hi to everybody

Homework Statement

Well I need to identify the forces acting on the bodies using free body diagramas, it´s not necessary to calculate anything, it´s only to learn about free body diagrams.

I will write my thoughts about the FBD and I will appreciate a lot if you see that I´m wrong in some part of the reasoning, or the forces are incorrect, that you correct me to show the correct FBD.

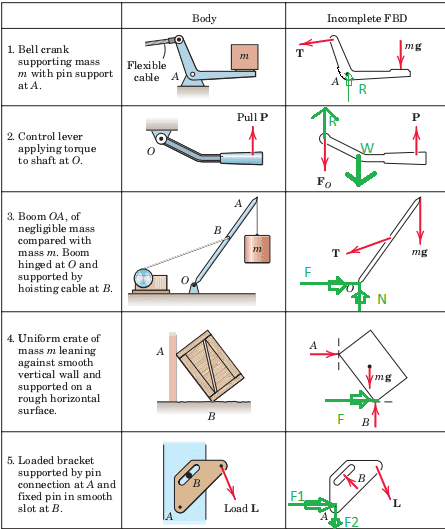In this first exercise I have the body on the left and an INCOMPLETE (but right) free body diagram on the right which I should modify to show all the forces. The red lines are given, I used green lines to include any extra forces which may be on the system.1.-
On the first one I think that the reaction force R it´s only perpendicular to A, the horizontal component of the force T will not have a reaction at A towards the opposite side, it will create a moment that will try to rotate the bell crank, and since the bell crank can rotate about A there won´t appear any reaction force on the horizontal axis.2.-
I was not sure about this one, on the incomplete FBD there is a F0 force downwards that I think it´s incorrect, that´s why I drew the reaction force R, I added the weight of the control lever. But the exercise says it´s an incomplete FBD but the given forces should be correct, WHy is there an external F0 force acting downwards?

3.-
I only need to add the reaction forces at O, which are friction to the right opposite to the horizontal compoment of the T force, and the normal force N, that acts against the weight mg and the vertical component of the force T.

4.-
I only need to add the friction force F because the surface is rough.

5.-
I´m not sure but I think that the pin connection at A is fixed and the brown body cannot rotate about A so there will appear two reaction forces F1, F2. I choosed those senses because I think they will act against a clockwise moment created by L around B, that´s why I think reaction F2 will point downwards, and F1 to the right.

Do you think I´m right? Do you see any mistakes? Am I missing any forces?

--------------------------------------------------------------------------------------

Now we have an incomplete or WRONG FBD on the right with red lines, so it will be more difficult to show how the forces are working on the system, I draw the correct FBD with green lines.

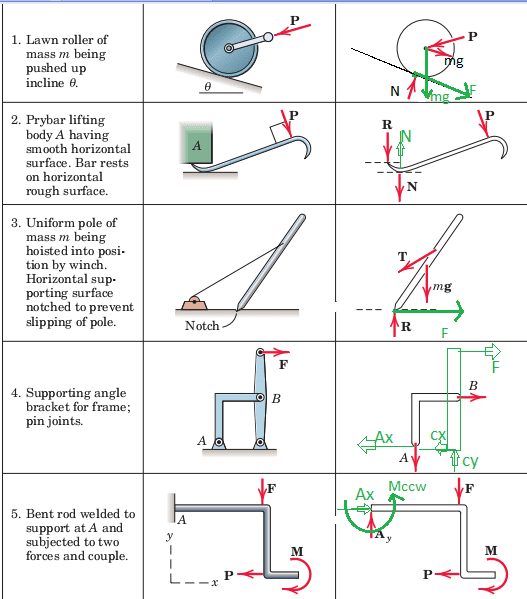
1.- Obviously mg is wrong, so I drew mg with the green line pointing downwards. I added too the friction force F pointint to the right because the wheel is being pushed up.

2.- I think that R and P are correct, but N should be in the opposite sense, so I drew that on the green line.

3.- I think that there should be a friction force F created by the notch at the ground.

4.- First of all I think there is not any external force at B, so that is wrong.

At the pionts A and C I have doubts, not sure about the sense.

There is not any vertical force on the body, since the mass is not considered, but I think that due to the force F the body will "try" to rotate around point C, raising point A, so the sense of the reaction at A will go downwards, but I´m not sure about this.

Just the opposite will happen at C to counteract the vertical force at A.

I know that this arguments are not too good, I´m sorry, I´m very curious about the correct answer.

I drew Ax and Cx opposite to force F because the equation for the x-axis should be zero.

5.-

Well I think that I need an Ax force opposite to P, and a counter clockwise moment at A to counteract the moment M, red circle.

Finally on the third exercise I need to draw everything, the free body diagram, and all the forces acting on it.

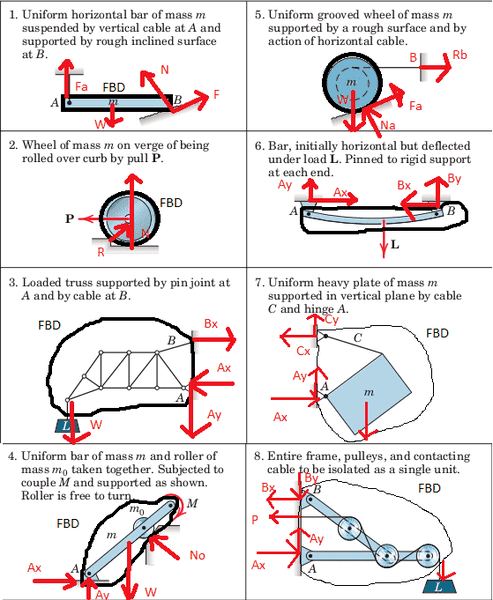
1.- With a thick black line I draw the free body diagram FBD which isolates the body from the exterior world.

In this case the body is the rectangular blue bar, and the forces acting on it are weight W acting at the center of the body, normal N and friction F forces at B, and the vertical Fa force at A.

2.- Obviously the body is the wheel, and I just added to the force P the reaction R and the normal force N.

3.- I show with the black line the fbd, the weight W of the load L is acting on the body, and that will try to rotate the body around A, trying to tear the body from B, that´s why I used opposite senses for Bx and Ax, it´s like A it´s the rotating axis. I´m not sure about the sense of Ay, maybe it´s opposite to the sense I drew.

4.- Well the weight W it´s obvious, I didn´t draw the weight of the mass m0 because the picture was too small. Those are easy ones, with the normal No, but there is a moment M and I think that the joint at A cannot create a moment M' to counteract that, the force No will be the one responsible to create a counter clock wise moment. So at A there are only reaction forces, I wasn´t sure about their sense.

I drew Ay pointing upwards to counteract the weights, and Ax positive because I think the moment M will try to rotate the bar around the ground at the roller so A would ascend to the left. Not sure about this.

5.- Well this seems an easy one I add the friction Fa because the surface is rough, normal Na, the weight and the tension Rb.

6.- If the bar wouldn´t be deflected obviously there wouldn´t be the two forces Ax and Bx, I think that the deflected bar is pushing outwards, that´s why the forces Ax and Bx are pointint inwards, but I´m not sure.

7.- Here forces Cx and Cy look like pretty easy, but at A I´m not sure about the sense of the Ay force, Is it pointing upwards? Ax and Cx have opposite senses because the body will try to rotate around A, tearing the body from C and pushing it against the wall at A.

8.- The same happens here with Bx, P and Ax, they have opposite senses.

I have doubts about the sense of By and Ay.

Thanks for arriving here :)

 

[voko]

I really do think this is far too many tasks for a single post or thread.

Let me address the first batch.

#2, #3, #4 and #5 are incorrect to a varying degree.

In #2, you are ignoring that the shaft might exert counter-torque on the lever; plus I think the mass of the lever should be neglected.

In #3, you don't have any friction. Rather, the pin's reaction has two components.

In #4, think again about the direction of the force of friction.

In #5, the body CAN rotate about A - it is a pin joint after all; but the rotation is prevented by the other pin. You actually did draw everything correctly, it is your reasoning that is wrong.

 

[jonjacson]

I really do think this is far too many tasks for a single post or thread.
Let me address the first batch.
#2, #3, #4 and #5 are incorrect to a varying degree.
In #2, you are ignoring that the shaft might exert counter-torque on the lever; plus I think the mass of the lever should be neglected.
In #3, you don't have any friction. Rather, the pin's reaction has two components.
In #4, think again about the direction of the force of friction.
In #5, the body CAN rotate about A - it is a pin joint after all; but the rotation is prevented by the other pin. You actually did draw everything correctly, it is your reasoning that is wrong.

Thanks Voko.

Some days ago I had doubts about writing one or three threads and I wasn´t sure about what to do, I believed that they were similar and opened only this thread, but from now on I´ll open one thread for every problem and it´ll be more delimited.

2.- So on the second there sould be a reacting clockwise moment at O? In that case why is F0 there?

Or Do you mean that F0 is creating the counter-torque?

If that is the case the given FBD is complete, and we should not need to add anything to it?

3.-Ok, yes there is not one surface against another, this is a different situation.

4.- Ups, it´s oppsite, thanks.

5.- I see, now this example is clear.

THank you!

 

[voko]

2.- So on the second there sould be a reacting clockwise moment at O? In that case why is F0 there?

You should not be asking me :) If unsure, write down the equilibrium equations and see what forces and couples must be there to make them consistent.

But in this particular case, you could use your intuition. The force on the lever has a non-zero moment about the shaft, and the shaft's reaction force has zero moment about itself, so it has to have a couple independently of the force, to balance the applied moment. It has to have a reaction force, too, because the couple alone cannot offset the applied force.

 

[jonjacson]

You should not be asking me :) If unsure, write down the equilibrium equations and see what forces and couples must be there to make them consistent.

But in this particular case, you could use your intuition. The force on the lever has a non-zero moment about the shaft, and the shaft's reaction force has zero moment about itself, so it has to have a couple independently of the force, to balance the applied moment. It has to have a reaction force, too, because the couple alone cannot offset the applied force.

I should! because you always answer in my threads .

Now seriously, I´ll do what you say, if there are doubts with the fbd I´ll use the equations to understand what happens.

My intuition is a complete failure, without your beautiful explanation I had never imagined that.

THank you!

 

[voko]

Here is one tip for your intuition: planar static problems always boil down to THREE equations (two for force components, one for moments). That means you have to have three unknowns to satisfy these equations. Each of those unknowns can be a force or a couple.

Tip #2. Sometimes it may seem that you have more than 3 unknowns. In this case, if the problem is supposed to be solvable, it WILL have some other conditions that you can translate into additional equations.

 

[jonjacson]

Those tips will be in my pocket since now.