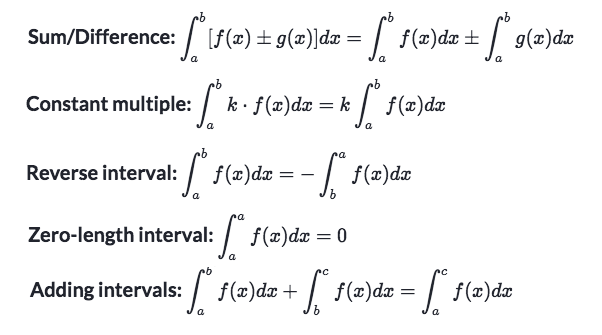The discussion centers on the properties of definite integrals, specifically the relationship between integrals with varying limits. The equation $\displaystyle \int_b^x g(t) \, dt = -\int_x^b g(t) \, dt$ is established as a fundamental property, leading to the conclusion that $\displaystyle \int_a^x g(t) \, dt - \int_b^x g(t) \, dt = \int_a^b g(t) \, dt$. This demonstrates the importance of understanding the behavior of integrands as functions of \(x\) and their limits in calculus.
PREREQUISITESStudents preparing for the AP Calculus exam, educators teaching calculus concepts, and anyone looking to deepen their understanding of integration limits and properties of definite integrals.
| $\displaystyle \int_b^x g(t) \, dt +\int_x^b g(t) \, dt=0$ |
