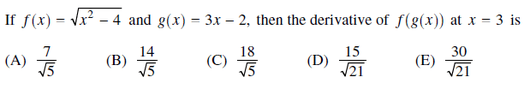2.8.218 AP Calculus Exam f'(g(3))=

[karush]

View attachment 9229

image to avoid typos

Spoiler

first derive
$\displaystyle f(g(x))=\sqrt{(3x-2)^2-4}=\sqrt{9x^2-12x}=(9x^2-12x)^{1/2}$
then by chain rule
$\displaystyle f'(g(x))=\dfrac{3\left(3x-2\right)}{\sqrt{9x^2-12x}}$
finally plug in $x=3$
$\dfrac{3\left(3(3)-2\right)}{\sqrt{9(3)^2-12(x)}}=\dfrac{7}{\sqrt{5}}\quad (A)$ok I was concerned that this had a lot of time consuming steps which I left out most of them
possible a u substitution might be quicker but nor sure where to fit that.

 

[skeeter]

$f'[g(3)] \cdot g'(3)$

$f'(7) \cdot g'(3)$

$\dfrac{7}{\sqrt{45}} \cdot 3 = \dfrac{7}{3\sqrt{5}} \cdot 3 = \dfrac{7}{\sqrt{5}}$