Homework Help Overview
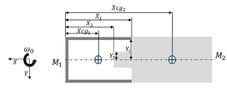
The discussion revolves around two rigid bodies, M1 and M2, that are connected and spinning around the Z-axis. At a specific moment, they are severed and given additional velocities in the X direction. The focus is on determining the minimum separation speed required to prevent collision between the bodies after they disconnect.
Discussion Character
- Exploratory, Assumption checking, Problem interpretation
Approaches and Questions Raised
- Participants explore the conditions under which the bodies will not collide after being severed. Questions arise regarding the definitions of separation speed and the implications of the velocities given to the bodies. Clarifications are sought about the setup, including the significance of various coordinates and visual elements in the problem.
Discussion Status
The discussion is ongoing, with participants attempting to clarify the physical setup and the relationships between the velocities of the bodies. Some guidance has been offered regarding the equations of motion, but there is no consensus on the minimum separation speed or the exact nature of the trajectories involved.
Contextual Notes
There is uncertainty regarding the definitions of the coordinates and the physical representation of the bodies in the problem. Participants are questioning the assumptions about the motion and the effects of the severing action on the bodies' trajectories.