- #1
abro
- 20
- 0
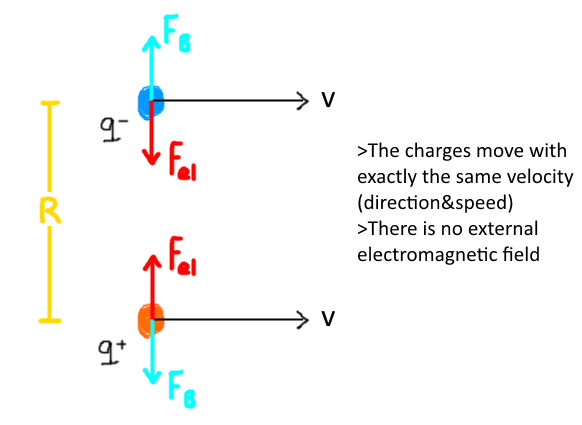
Consider two equal and opposite charges moving in the same direction and velocity v0, and are separated a distance R. There will always be an attractive electromagnetic force Fel=q2/(4πεR2), but when they are moving, they will produce a magnetic field B=μqv/(4πR2), and thus a repulsive magnetic force FB=Bqv.
I tried finding the velocity at which these forces are balanced;
Fel=FB
q2/(4πεR2)=μq2v2/(4πR2)
v0=1/√(ε0μ0), which turns out to be the speed of light.
I find this result very surprising; the forces will be canceled out when only the velocity is the speed of light, and the charge and distance can be anything. Does this mean like light has two very small charges with equal spins (1/2+1/2=1) and no mass and thus can interact electromagnetically?
Edit: Here is a picture to clarify what I mean.
I tried finding the velocity at which these forces are balanced;
Fel=FB
q2/(4πεR2)=μq2v2/(4πR2)
v0=1/√(ε0μ0), which turns out to be the speed of light.
I find this result very surprising; the forces will be canceled out when only the velocity is the speed of light, and the charge and distance can be anything. Does this mean like light has two very small charges with equal spins (1/2+1/2=1) and no mass and thus can interact electromagnetically?
Edit: Here is a picture to clarify what I mean.
Last edited: