2 Questions About the Gyroscope Effect

[Johnls]

I'm talking here about this situation:

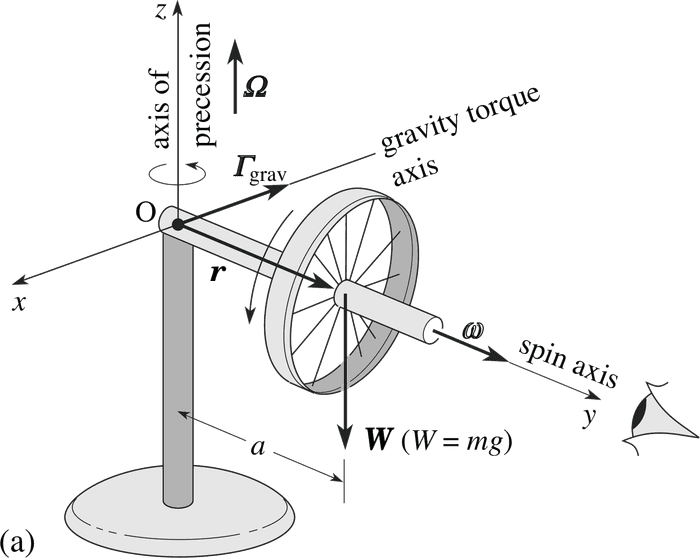
The explanation which is usually given as to why there is a precession, is that the torque is perpendicular to the angular momentum and the angular momentum changes in the direction of the torque.
A few things I don't understand about it:

1. The torque is relative to point O but the angular momentum is relative to the center of the wheel. When you derive that torque is the change in the angular momentum, don't you assume that they are both calculated relative to the same point?

2. Why doesn't it work for low angular momentums?

 

[jbriggs444]

1. The torque is relative to point O but the angular momentum is relative to the center of the wheel. When you derive that torque is the change in the angular momentum, don't you assume that they are both calculated relative to the same point?

Two points...

A torque can be viewed as a "couple" -- a pair of equal and opposite forces separated by a distance that is not parallel to the forces. It does not matter where you choose to place the reference point when calculating the torque from a couple. You always get the same answer.

Point O lies on the axis of rotation anyway.

2. Why doesn't it work for low angular momentums?

The idea that the angular momentum of a gyroscope is purely horizontal, that it does not deflect downward at all under a vertical force and that the motion associated with the precession has no associated angular momentum is an approximation. For a rapidly spinning gyroscope, it is a good approximation. In first year physics courses one is usually exposed to angular momentum primarily as it applies in two dimensions. In that setting, one considers the gyroscope to be rotating in two dimensions and precessing in the third.

The full three dimensional treatment involves the notion of a "nutation" and analysis using tensors.

One simple way of seeing that the precession model cannot work for low angular momentum is to consider what happens as the rotation rate gets lower and lower. The precession rate gets higher and higher. If you get to a point where the precession rate is higher than the rotation rate, it's pretty clear that you're not considering a gyroscope that is spinning on its intended axis. Instead, it is rotating around a different instantaneous axis. And that axis may keep changing over time.

A gyroscope that is not spinning at all does not precess infinitely fast. It just flops down.

 

[Johnls]

Two points...

A torque can be viewed as a "couple" -- a pair of equal and opposite forces separated by a distance that is not parallel to the forces. It does not matter where you choose to place the reference point when calculating the torque from a couple. You always get the same answer.

Point O lies on the axis of rotation anyway.The idea that the angular momentum of a gyroscope is purely horizontal, that it does not deflect downward at all under a vertical force and that the motion associated with the precession has no associated angular momentum is an approximation. For a rapidly spinning gyroscope, it is a good approximation. In first year physics courses one is usually exposed to angular momentum primarily as it applies in two dimensions. In that setting, one considers the gyroscope to be rotating in two dimensions and precessing in the third.

The full three dimensional treatment involves the notion of a "nutation" and analysis using tensors.

One simple way of seeing that the precession model cannot work for low angular momentum is to consider what happens as the rotation rate gets lower and lower. The precession rate gets higher and higher. If you get to a point where the precession rate is higher than the rotation rate, it's pretty clear that you're not considering a gyroscope that is spinning on its intended axis. Instead, it is rotating around a different instantaneous axis. And that axis may keep changing over time.

A gyroscope that is not spinning at all does not precess infinitely fast. It just flops down.

First of all, thanks for the reply!
Could you please expand a little bit on how torque can be viewed as a "couple"? How can I do this conversion? How does it relate to the Gyro example?

 

[jbriggs444]

First of all, thanks for the reply!
Could you please expand a little bit on how torque can be viewed as a "couple"? How can I do this conversion? How does it relate to the Gyro example?

For the gyroscope, you have an upward force at point O from the support and a downward force from gravity at the center of gravity (a distance r from point O).

Pick any origin you like and compute the torque from the force at point O plus the torque from the force at the center of gravity. Then pick a different origin and compute it again. The two forces are a "couple" and the net torque they produce will be independent of the origin that you pick.

 

[Johnls]

For the gyroscope, you have an upward force at point O from the support and a downward force from gravity at the center of gravity (a distance r from point O).

Pick any origin you like and compute the torque from the force at point O plus the torque from the force at the center of gravity. Then pick a different origin and compute it again. The two forces are a "couple" and the net torque they produce will be independent of the origin that you pick.

Oh I see... Thanks!