Mech King
- 69
- 0
Hey guys,
I'm just pondering a beam problem fir a structure that I'm analysing. It appears statically indeterminate to me? The beam is bolted to a support at locations A,B & C. There are two point loads between span B-C.
There are no symmetrical distances or support locations etc.
Initially, I just ignored span A-B, as I assumed that the load would not transfer to the far left hand end at A, because it is rigidly fixed at B & C? Is this incorrect?
Now I am thinking that I do need to consider the left hand span AB.
I thought that I could assume "A" does not support the beam, then calculate the deflection of the beam at the left hand side in the unsupported region and then calculate what the restoring force would need to be to prevent such deflection, therefore calculating reaction A, and then take moments to calculate reactions B and C?
Or is there a better approach? I'm really getting a bit stuck here and would appreciate any guidance!
Many thanks
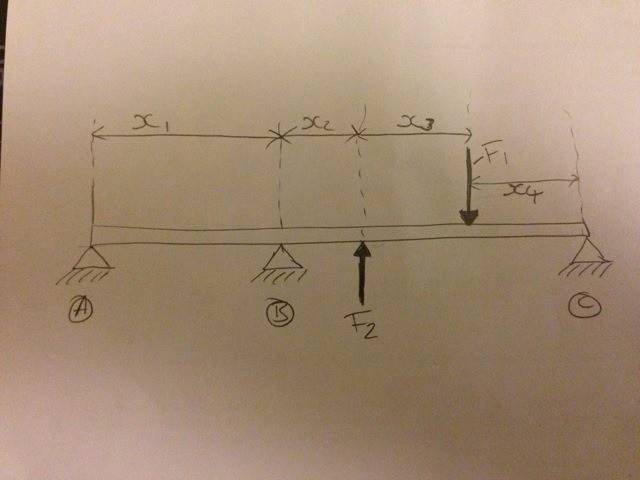
I'm just pondering a beam problem fir a structure that I'm analysing. It appears statically indeterminate to me? The beam is bolted to a support at locations A,B & C. There are two point loads between span B-C.
There are no symmetrical distances or support locations etc.
Initially, I just ignored span A-B, as I assumed that the load would not transfer to the far left hand end at A, because it is rigidly fixed at B & C? Is this incorrect?
Now I am thinking that I do need to consider the left hand span AB.
I thought that I could assume "A" does not support the beam, then calculate the deflection of the beam at the left hand side in the unsupported region and then calculate what the restoring force would need to be to prevent such deflection, therefore calculating reaction A, and then take moments to calculate reactions B and C?
Or is there a better approach? I'm really getting a bit stuck here and would appreciate any guidance!
Many thanks