Cantilever statically indeterminate beam with point load

In summary, The conversation is about finding the equation for deflection in a statically indeterminate cantilever beam with an attached point load. The built-in end has both deflection and slope equal to zero, while the propped end only has deflection equal to zero. The poster is having trouble finding the correct equation and asks for help. SteamKing provides clarification on the boundary conditions and asks for the poster's calculations. The poster apologizes for the late reply and attaches part of their calculations for clarification.
  • #1
sara291
4
0
hi
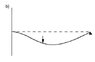
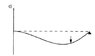
please if anyone can tell me how i can get the following equation (attachments) of deflection for statically indeterminate cantilever beam with point load (attachments). I'm not an engineering student and having difficulty in coming up with boundary conditions.
looking for help. thanks
 

Attachments

  • Capture.JPG
    Capture.JPG
    11.9 KB · Views: 548
  • Capture2.JPG
    Capture2.JPG
    4.5 KB · Views: 648
  • Capture3.JPG
    Capture3.JPG
    4 KB · Views: 585
Engineering news on Phys.org
  • #2
At the built-in end, the deflection and slope of the beam are both equal to zero. At the propped end, only the deflection is equal to zero.
 
  • #3
thank you SteamKing. it means at clamped end y(x) & dy/dx = 0 and propped end only dy/dx=o.
 
  • #4
sara291 said:
thank you SteamKing. it means at clamped end y(x) & dy/dx = 0 and propped end only dy/dx=o.

You got it half right. At the propped end, the deflection y = 0, not the slope dy/dx, as can be seen by inspection of the figure.
 
  • #5
i tried these condition to find the deflection equation (eq image in thumbnail) using eq M=EI d^2y/dx^2, by integration method. but when i find the constants of integration by applying these BC and put their values i got zero instead of above equation. please help!
 

Attachments

  • Capture.JPG
    Capture.JPG
    40.5 KB · Views: 4,595
  • #6
Can you post your calculations? It might be easier than trying to go through the whole exercise from scratch.
 
  • #7
thank you SteamKing, and sorry for late reply, part of my calculation is in attachment. i hope you understand my writing...
 

Attachments

  • Image0624.jpg
    Image0624.jpg
    19.3 KB · Views: 581
  • Image0625.jpg
    Image0625.jpg
    14.9 KB · Views: 562

Related to Cantilever statically indeterminate beam with point load

What is a cantilever statically indeterminate beam?

A cantilever statically indeterminate beam is a structural element that is supported on only one end and has more unknown reactions than the number of equilibrium equations available to solve for them. This means that the beam's reactions and internal forces cannot be determined using basic statics equations alone.

How is the load on a cantilever statically indeterminate beam calculated?

The load on a cantilever statically indeterminate beam can be calculated using the method of consistent deformations or the slope-deflection method. Both methods involve setting up equations based on the beam's geometry and material properties, and then solving for the unknown reactions and internal forces.

What is the effect of a point load on a cantilever statically indeterminate beam?

A point load on a cantilever statically indeterminate beam will cause the beam to deflect and experience internal bending moments and shear forces. The magnitude and distribution of these internal forces will depend on the location and magnitude of the point load, as well as the beam's geometry and material properties.

Can a cantilever statically indeterminate beam withstand a point load?

Yes, a cantilever statically indeterminate beam is designed to withstand various types of loads, including point loads. However, the beam's ability to resist the load will depend on its strength and stiffness, as well as the magnitude and location of the point load.

How can the reactions and internal forces of a cantilever statically indeterminate beam be determined?

The reactions and internal forces of a cantilever statically indeterminate beam can be determined by solving the equations of equilibrium and compatibility using the method of consistent deformations or the slope-deflection method. Alternatively, computer software programs can also be used to analyze the beam and determine its reactions and internal forces.

Similar threads

What is the best beam design for my aluminum tandem axle trailer?
    • Mechanical Engineering
Replies
33
Views
3K
Cantilever beam deflection with point mass and point load at the end
    • Mechanical Engineering
Replies
3
Views
2K
Deflection of a cantilever beam with applied tension at the free end
    • Mechanical Engineering
Replies
9
Views
2K
Big Robot- Lattice boom crane - calculating maximum stress
    • Mechanical Engineering
Replies
2
Views
704
Pure bending of a perfectly elastic cantilever beam
    • Mechanical Engineering
Replies
5
Views
1K
Complex frames - analytical calculations
    • Mechanical Engineering
Replies
6
Views
1K
Deflection of partially loaded cantilever beam with non-homogeneous EI
    • Engineering and Comp Sci Homework Help
Replies
3
Views
394
Boundary conditions in Ansys
    • Mechanical Engineering
Replies
3
Views
2K
Cantilever Beam Small Deflection Approximation
    • Mechanical Engineering
Replies
8
Views
3K
Contact Stresses in Cantilevered Journal Bearing
    • Mechanical Engineering
Replies
1
Views
987

Hot Threads

Recent Insights

Back
Top