3-D Planar Method of Images Boundary Problem

[sdefresco]

Homework Statement

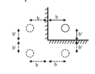
Given 3, grounded conducting planes at x=0,y=0,z=0, and a charge q at ro=(xo,yo,zo), determine V(x,y,z) using method of images.

Relevant Equations

None.

I understand the idea of the method of images, and its clever use of uniqueness to determine V(x,y,z) for non-trivial systems.

My question now is simply about guidance for obtaining the effective "image" of this system, as it is clearly more complicated than the 2-plane analogue (in which there are 3 imaged charges - -q below z=0, -q left of x=0, and q at (-xo,-zo) (photo I linked in the post) .

With the introduction of the x-z plane, continuing the image as such does not result in a sufficient V(x,y,z).

I understand that the goal is to recreate the boundary conditions (as a solution adhering to them is the only solution), but fulfilling all three at once has proven challenging.

So far, I know that putting -q directly on the other sides of the three planes causes an obvious issue in which their potentials interact, unfulfilling the boundary conditions. Obviously, no points can be placed inside our R.O.I.

 

[BvU]

continuing the image as such

Could you be more specific ? What charge at (x₀,-y₀,z₀) etc.

putting -q directly on the other sides of the three planes

That is not what was done to go from 1 to 2 planes, as you so nicely describe, ... so ...

 

[PhDeezNutz]

Let’s continue this trend. Forgive me if I’m wrong. I’m new here.

For a single plane the effective image configuration was a dipole correct?

For two planes it’s a quadrupole

For three planes it should be an octupole.