jumi
- 26
- 0
Ok, I have this circuit, and I'm trying to devise a way to create an 8x8 matrix for any given combination of target qubit and controlled qubit.
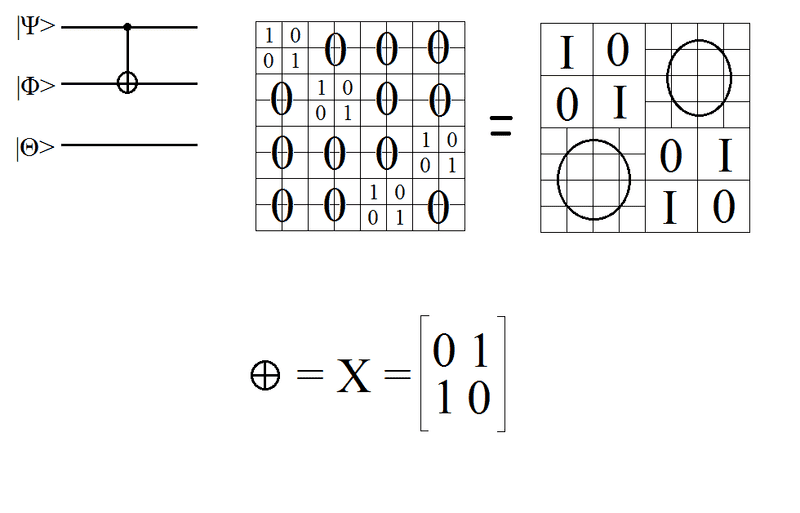
(I is the identity matrix, and X is the CNOT operator)
I want it to also include the qubit that passes through untouched because I'm trying to write a program that takes a given state of 3 qubits and runs it through the above circuit.
As of now, for any combination of target and control qubit, I've generated the 8x8 matrices on paper, but I wondering if there's an easier way to generate each case?
If I had to, I suppose I could "brute force" code each individual case (i.e. 1 on 2, 1 on 3, 2 on 3 and their opposites), but it seems like I'm missing something quite easy that wouldn't require that...
Thanks in advance.
(I is the identity matrix, and X is the CNOT operator)
I want it to also include the qubit that passes through untouched because I'm trying to write a program that takes a given state of 3 qubits and runs it through the above circuit.
As of now, for any combination of target and control qubit, I've generated the 8x8 matrices on paper, but I wondering if there's an easier way to generate each case?
If I had to, I suppose I could "brute force" code each individual case (i.e. 1 on 2, 1 on 3, 2 on 3 and their opposites), but it seems like I'm missing something quite easy that wouldn't require that...
Thanks in advance.