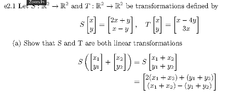-307.17.1 Show that S and T are both linear transformations

[karush]

View attachment 8994

ok this is a clip from my overleaf homework reviewing

just seeing if I am going in the right direction with this

their was an example to follow but it also was a very different problem

much mahalo

 

[Evgeny.Makarov]

The last two lines have two equalities. Their status is not clear. Please say for each equality if it is something you plan to prove, something you assume, or something you have proved and how (by definition, by laws of algebra, etc.).

The claim that $S$ is a linear transformation requires a proof, and a proof is not simply some collection of formulas. A proof is an argument that starts with assumptions and arrives and the desires conclusion. proofs are best expressed using text in a natural language (English) written in complete grammatical sentences.

 

[karush]

The last two lines have two equalities. Their status is not clear. Please say for each equality if it is something you plan to prove, something you assume, or something you have proved and how (by definition, by laws of algebra, etc.).

The claim that $S$ is a linear transformation requires a proof, and a proof is not simply some collection of formulas. A proof is an argument that starts with assumptions and arrives and the desires conclusion. proofs are best expressed using text in a natural language (English) written in complete grammatical sentences.

View attachment 9009
ok here is the example I am trying to follow

 

[Evgeny.Makarov]

Yes, so far what you wrote is correct, and it follows the example.

 

[karush]

Yes, so far what you wrote is correct, and it follows the example.

Let
$S:\Bbb{R}^2\to \Bbb{R}^2$ and $T:\Bbb{R}^2 \to \Bbb{R}^2$ be transformations defined by
$\begin{bmatrix}
x\\y
\end{bmatrix}=
\begin{bmatrix}
2x+y \\
x-y
\end{bmatrix},
\quad T
\begin{bmatrix}x\\y
\end{bmatrix}=
\begin{bmatrix}x-4y\\3x
\end{bmatrix}$
Show that S and T are both linear transformations
$\begin{align*}\displaystyle
S\left(\left[\begin{array}{} x_2 \\ y_2 \end{array}\right]
+\left[\begin{array}{} x_2\\y_2\end{array}\right]\right)
&=S\left[\begin{array}{}x_1+x_2\\y_1+y_2\end{array}\right]\\
&=\left[\begin{array}{c}2(x_1+x_2)+(y_1+y_2) \\ (x_1+x_2)-(y_1+y_2) \end{array}\right]\\
&=\left[\begin{array}{c} 2x_1+2x_2\\x_1+x_2 \end{array}\right]
+\left[\begin{array}{c}y_1+y_2\\-y_1-y_2) \end{array}\right]
\end{align*}$
ok for some reason I can't see how this is going to preserve addition
or is there another way to show transformaton?

 

[Evgeny.Makarov]

The last line should be

$$\begin{bmatrix}2x_1+y_1\\x_1-y_1\end{bmatrix}+\begin{bmatrix}2x_2+y_2\\x_2-y_2\end{bmatrix}$$.

 

[karush]

ok here is the whole story... typo's maybe
$S:\Bbb{R}^2\to \Bbb{R}^2$ and $T:\Bbb{R}^2 \to \Bbb{R}^2$ be transformations defined by
$\begin{bmatrix}x\\y \end{bmatrix}=
\begin{bmatrix}2x+y \\x-y \end{bmatrix},
\quad T\begin{bmatrix}x\\y \end{bmatrix}=
\begin{bmatrix}x-4y\\3x \end{bmatrix}$
Show that S and T are both linear transformations
$\begin{align*}\displaystyle
S\left(\left[\begin{array}{} x_2 \\ y_2 \end{array}\right]
+\left[\begin{array}{} x_2\\y_2\end{array}\right]\right)
&=S\left[\begin{array}{}x_1+x_2\\y_1+y_2\end{array}\right]\\
&=\left[\begin{array}{c}2(x_1+x_2)+(y_1+y_2) \\ (x_1+x_2)-(y_1+y_2) \end{array}\right]\\
&=\begin{bmatrix}2x_1+y_1\\x_1-y_1\end{bmatrix}+\begin{bmatrix}2x_2+y_2\\x_2-y_2\end{bmatrix}\\
&=S \begin{bmatrix}x_1\\y_1\end{bmatrix} +S\begin{bmatrix} x_2\\y_2\end{bmatrix}\end{align*}$
S preserves addition, If c is any scalar.
$S\left(c\begin{bmatrix} x_1\\y_1\end{bmatrix}\right)
=S\begin{bmatrix} cx_2\\cy_2 \end{bmatrix}
=\begin{bmatrix} 2cx+cy \\ cx-cy \end{bmatrix}
=c\begin{bmatrix} 2x+y \\ x-y \end{bmatrix}
=cS\begin{bmatrix} x_1\\y_1\end{bmatrix}$
and consequently T preserves scalar multiplication.

 

[karush]

ok (b) and (c) came with this problem, but I think I got them ok but wanted to post it.(b) Find $ST
\begin{bmatrix} x\\y
\end{bmatrix}$
$$ST\begin{bmatrix}x\\y\end{bmatrix} =S\left(T\begin{bmatrix}
x-4y\\3x
\end{bmatrix}\right)
=\left[\begin{array}{c}
2(x-4y)+3x \\ x-4y-3x
\end{array}\right]$$
and $T^2
\begin{bmatrix} x\\y
\end{bmatrix}$
$$T^2\left(\left[\begin{array}{c}
x \\ y \end{array}
\right]\right)
=T\left(T\left(\left[\begin{array}{c}
x \\ y
\end{array}\right]\right)\right)
=T\left(\left[\begin{array}{c}
x-4y\\3x
\end{array}\right]\right)
=\left[\begin{array}{c}
x-4y-4(3x) \\ 3(x-4y)
\end{array}\right]$$
(c) Find the matrices of S and T with respect to the standard basis for $\Bbb{R}^2$.
$$\displaystyle\left[S\right]_\infty^\infty
=\left[\begin{array}{cc}
2&1\\1&-1
\end{array}\right], \quad
\left[T\right]_\infty^\infty
=\left[\begin{array}{cc}
1&-4\\3&0
\end{array}\right]$$