3D Laplace solution in Cylindrical Coordinates For a Hollow Cylindrical Tube

[jkthejetplane]

Homework Statement

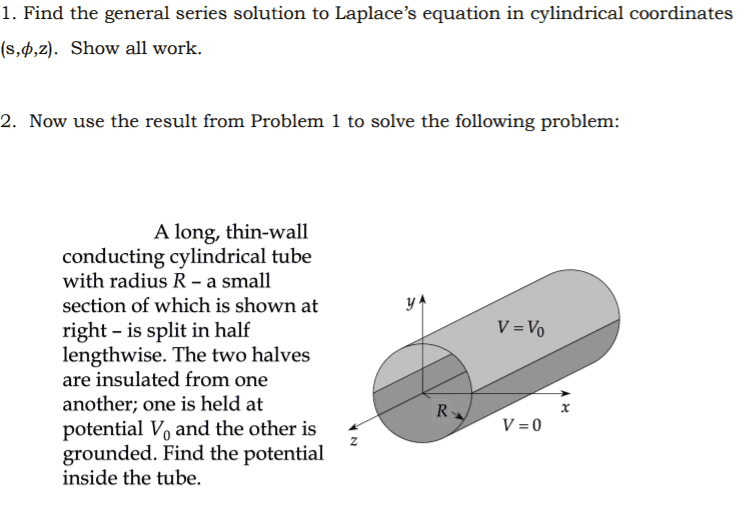
Find the general series solution for laplace in cylindrical coordinates

Relevant Equations

for this i have always used (s,phi,z)

Here is the initial problem and my attempt at getting Laplace solution. I get lost near the end and after some research, ended up with the Bessel equation and function. I don't completely understand what this is or even if this i the direction I go in.
This is a supplemental thing that I want to nail down for review to get my brain up to speed again for this semester

 

[pasmith]

You are missing a term from your final equation.

The solution must be periodic in $\phi$, so the dependence will be $\Phi'' = -n^2\Phi$. You do then have $Z'' = CZ$, but at this point there's no reason to believe that $C \geq 0$. So your radial dependence satisfies $$s^2 S'' + s S' + (Cs^2 - n^2)S = 0.$$ Setting $k = |C|^{1/2}$ and $x = ks$ turns this into $$x^2 \frac{d^2S}{dx^2} + x \frac{dS}{dx} + (\operatorname{sgn}(C) x^2 - n^2)S = 0$$ which is the Bessel equation if $C > 0$ and the modified Bessel equation if $C < 0$. If $C = 0$ then the dependence on $z$ is $Az + B$ and the radial dependence is $s^\alpha$ where $\alpha$ depends on $n$.

The Bessel functions are oscillatory with amplitude decaying to zero as $x \to \infty$. The Bessel function of the first kind ,$J_n$, is bounded at the origin with $J_0(0) = 1$ and $J_n(0) = 0$ for $n \geq 1$. The Bessel function of the second kind, $Y_n$, blows up at the origin. The modified Bessel functions are monotonic and positive with the modified function of the first kind, $I_n$, being bounded at the origin with $I_0(0) = 1$ and $I_n(0) = 0$ for $n \geq 1$ and increasing without limit as $x \to \infty$, and the modified function of the second kind, $K_n$, blowing up at the origin and decaying to 0 as $x \to \infty$.