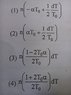Problem Related to Beat Frequency of a hollow tube

[digitomega]

Homework Statement

Q. A hollow metallic tube closed at one end produces resonance with a tuning fork of frequency n at temperature T. The temperature of the tube is increased by dT. If the coefficient of thermal expansion of the tube metal is alpha, the beat frequency will be - (there are 4 option in the attached image)

Homework Equations

Frequency for a tube closed at one end - n=v/(4l),3v/(4l)...
[/B]

The Attempt at a Solution

I have no idea ho to get the solution in terms of temperature and coefficient of thermal expansion.
[/B]

 

[haruspex]

I'm not sure I understand the question.
It is a simple matter to find the change in length of the tube and consequent change in frequency, but a beat requires two frequencies at once. Seems to me there will be one frequency at one temperature and a different frequency at the raised temperature.

Doh! Forgot about the tuning fork. Thanks TSny.

 

[TSny]

I think that when the temperature of the tube is raised, the tuning fork still vibrates at its original frequency. I guess you assume that the fork can still excite the same mode in the tube, but now the mode has a slightly different frequency than the tuning fork.

 

[digitomega]

You are right haruspex. I also tried finding frequency in the two cases but the required answer is in terms of T and alpha. I can get alpha in the answer expression but I have no idea about how to get T in the expression.

 

[TSny]

I have no idea about how to get T in the expression.

Assume the gas inside the tube is also heated.

 

[haruspex]

You are right haruspex. I also tried finding frequency in the two cases but the required answer is in terms of T and alpha. I can get alpha in the answer expression but I have no idea about how to get T in the expression.

Please post some working...
How does the temperature relate to the length?
How does the wavelength relate to the length?
How does the temperature relate to the speed of sound in the air?
How does the frequency relate to the wavelength and the speed of sound?

 

[digitomega]

Please post some working...
How does the temperature relate to the length?
How does the wavelength relate to the length?
How does the temperature relate to the speed of sound in the air?
How does the frequency relate to the wavelength and the speed of sound?

For a tube closed at one end-
1/λ = v/4l (λ= wavelength and v= speed of sound).
Increasing the temperature ultimately increases speed as well as frequency of sound.
for sound there is the relation n=c/λ. (n=frequency, c=speed of sound,λ=wavelength)
As for length and temperature relation, increasing temperature increases length.

Problem is I don't know and can't find how to replace l and v in the expression I am getting for the beat frequency to make it like one of the 4 options.

 

[haruspex]

1/λ = v/4l (λ= wavelength and v= speed of sound).

Something wrong there. It doesn't make sense dimensionally.

Increasing the temperature ultimately increases speed as well as frequency of sound.

Well, it changes the speed of sound. It does not directly change the frequency. What is the equation?

Once you have the right relationship in each case, you need either to write a second copy of each, using different symbols for the changing variables (e.g. T for initial temperature, T' for final temperature, etc.) or write the "delta" equations, e.g. how the change in temperature, ΔT, relates to the change in speed of sound, Δc.