3D shapes with perfect polygons

[scott_alexsk]

Hello, (edit should be regular polygons in title)

I have been thinking a lot recently about 3D shapes formed by 2D regular polygons. I was asking myself if there would be any way to calculate the minimium number of regular polygons to form a complete 3D shape. It is fairly easy with an equilateral triangle, which requires 4 sides, and for a square, with 6, but when I got to pentagons many problems arised.

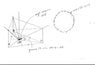
For one I was trying to calculate the angle the corners of 3 pentagons would have to be placed up agaisnt each other relative to a plane (see drawing). I ended up just assuming that the angle was 12, though I really have no idea, and continued with my estimates. So assuming that x (in the diagram) is 12 degrees, then I can calculate that the angle of each face to the other is about 156 degrees. With 156 I found the number of sides of a ploygon with those angles to be 15. From there I guesstimated that a pentagon forming a 3D shape by itself must have a minimum of around 80 faces.

Now I have several questions. Is my assumption that the angle x is 12, correct, if not how do I preform a correct calculation? Also what is the true number of sides a regular pentagon must have to form a 3D shape? Is there an equation which can identify the number of faces required for certain polygons to form 3d shapes? Finally, is there any way a single regular ploygon can approminate a sphere? Beyond a hexagon it is impossible to form 3D shapes since the measure of internal angles goes beyond 120, which means 3 corners cannot intersect.

Thanks,
-scott

Hopefully you can read this.

 

[Data]

The number of (convex) polyhedra you can get out of congruent regular polygons is quite limited (there are only 5).

http://en.wikipedia.org/wiki/Platonic_solid.

 

[scott_alexsk]

Yeah, I knew there would be only a few. But I still have one question. What is the angle that 3 corners of a pentagon have to be bent relative to a plane, (see drawing) to fit together?

Thanks,
-scott

 

[Data]

I can't see the drawing because it hasn't been approved yet . If you're talking about the angle I assume you're talking about then there is an expression for it on that page (search for "dihedral angle").

 

[scott_alexsk]

Thanks for the links and info Data.

-scott

 

[Doodle Bob]

The number of (convex) polyhedra you can get out of congruent regular polygons is quite limited (there are only 5).

http://en.wikipedia.org/wiki/Platonic_solid.

If you allow more than one type of regular polygon, you can get a few more. Look up: Archimedean solids.