karush
Gold Member
MHB
- 3,240
- 5
View attachment 9426
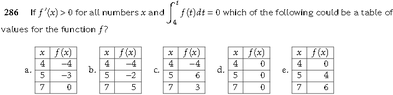
ok these always baffle me because f(t) is not known. however if $f'(t)>0$ then that means the slope is aways positive which could be just a line. but could not picture this to work in the tables.
Im sure the answer can be found quickly online but I don't learn by copy and paste. d was attractive but where would the slope be?
so any sugest..
ok these always baffle me because f(t) is not known. however if $f'(t)>0$ then that means the slope is aways positive which could be just a line. but could not picture this to work in the tables.
Im sure the answer can be found quickly online but I don't learn by copy and paste. d was attractive but where would the slope be?
so any sugest..