- #1
karush
Gold Member
MHB
- 3,269
- 5
309 average temperature
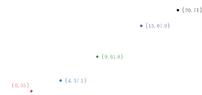
$$\begin{array}{|c|c|c|c|c|c|c|}
\hline
t\,(minutes)&0&4&9&15&20\\
\hline
W(t)\,(degrees Farrenheit)&55.0&57.1&61.8&67.9&71.0\\
\hline
\end{array}$$
The temperature of water in a tub at time t is modeled by a strictly increasing, twice-differentiable function W. where W(t) is measured in degrees Fahrenheit and t is measured in minutes.
At time $t=0$. the temperature of the water is $55^o F$.
The water is heated for 30 minutes, beginning at time $t=0$,
Values of $W(t)$ at selected times t for the first 20 minutes are given in the table above.
a. Use the data in the table to estimate W'(12).
b. Show the computations that lead to your answer. using correct units,
c. For $0\le t \le 20$ the average temperature of the water in the tub is
$\dfrac{1}{20}\int_0^{20} W(t)\, dt$
Does this approximation overoptimistic or underestimate the average temperature of the water over these 20 minutes? Explain.
ok not sure just what kind of equation we need for this since the points are close to a straight line
View attachment 9366
$$\begin{array}{|c|c|c|c|c|c|c|}
\hline
t\,(minutes)&0&4&9&15&20\\
\hline
W(t)\,(degrees Farrenheit)&55.0&57.1&61.8&67.9&71.0\\
\hline
\end{array}$$
The temperature of water in a tub at time t is modeled by a strictly increasing, twice-differentiable function W. where W(t) is measured in degrees Fahrenheit and t is measured in minutes.
At time $t=0$. the temperature of the water is $55^o F$.
The water is heated for 30 minutes, beginning at time $t=0$,
Values of $W(t)$ at selected times t for the first 20 minutes are given in the table above.
a. Use the data in the table to estimate W'(12).
b. Show the computations that lead to your answer. using correct units,
c. For $0\le t \le 20$ the average temperature of the water in the tub is
$\dfrac{1}{20}\int_0^{20} W(t)\, dt$
Does this approximation overoptimistic or underestimate the average temperature of the water over these 20 minutes? Explain.
ok not sure just what kind of equation we need for this since the points are close to a straight line
View attachment 9366
Attachments
Last edited: