4.1.310 AP calculus Exam Area under to functions

[karush]

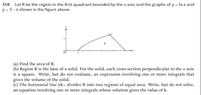
View attachment 9489
ok I got stuck real soon...

.a find where the functions meet $$\ln x = 5-x$$
e both sides
$$x=e^{5-x}$$ok how do you isolate x?

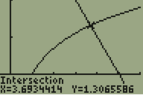
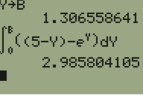
W|A returned $x \approx 3.69344135896065...$
but not sure how they got itb.?
c.?

 

[skeeter]

FYI, this is a calculator active problem ...

$y = \ln{x} \implies x = e^y$

$y = 5-x \implies x = 5-y$

$$R = \int_0^{1.3065586} (5-y) - e^y \, dy = 2.986$$

 

[karush]

so then we don't need to know x of the intersection

 

[skeeter]

so then we don't need to know x of the intersection

yes, you need both x and y coordinates of the intersection point ...

(a) can be done w/r to x or y ... I went w/r to y because it only requires a single integral expression

(b) requires x ... two integrals

(c) requires y

 

[karush]

ill go with c

 

[skeeter]

ill go with c

?

(c) is a free response question, not a choice